Scaling law

简单介绍Scaling law

Kaplan et al. (2020) （GPT3前）

作者想要像理想气体定律一样建立LLM的经验方程。通过实验拟合主要有以下结论：

• 性能影响因子：特定条件下模型最终性能（以cross entropy（L）度量）主要由衡量模型scale的三个参数计算量C（FLOPs）、参数量N和数据量D（tokens）决定，与模型架构的一些参数关系很小

  • 注意要求在同一类架构下比较，例如lstm和transformer的性能就有较大差别；而都是transformer时，调整MHA参数之类对最终结果影响就较小。

• 幂律关系：当C、N、D中任意两个参数不是性能bottleneck（可以看成无穷），则剩下的一个参数和模型性能L在相当大的范围内成负指数幂律关系

  • 注意这只是一种粗糙的理解，实际上有很多前提条件（例如对batchsize的要求等）
  • 由此得到的结论就是全力增大C、N、D即可提升模型性能

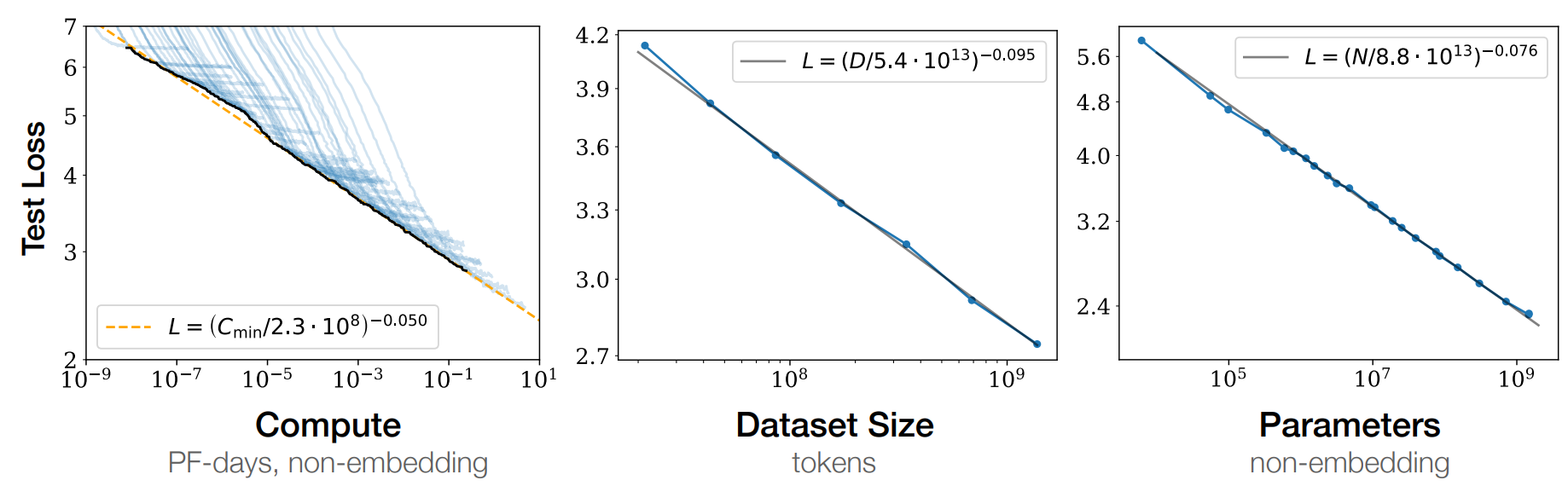
• 参数规模优先：在总算力预算固定时，最好用更大的模型在较小的数据上训练，这样即使未完全收敛也比小模型大数据训到完全收敛的性能好，即在N和D之间选择优先增大N
  • 当然这一点后来有更多讨论
• 跨模态适用性：图像视频等任务中也有类似规律
  • Baidu很久以前也有过类似的研究

Hoffmann et al. (2022)

这篇paper主要是针对“参数规模优先”进行的讨论，经实测发现：

• 总算力C固定，则最优的N和D都近似∝$\sqrt{C}$ （compute-optimal）
• 因此，当C提升时，N和D应当同等重要地大致成比例提升
• 基于此训出的Chinchilla（70B）比未充分训练（数据量偏少）的Gopher、GPT-3等性能更好

进一步讨论

• 即便D都是一样的，数据质量的影响仍然很大（PaLM，LLaMA，Qwen，etc）
• 上下文长度会影响分配规律（Gemini 1.5，GPT4.1，etc）
• multi modal有自己的分配方式
• CoT、tool use之类的能力只在N足够大时才突然出现