傅里叶光学3

对应第三章

Ch3 标量衍射理论基础

3.1 历史引言

• 区别于反射、折射（斯涅尔定律）、半影效应（发生于非点光源的情形，书上的图可能使人误解）
• 标量理论在这些情况下比较精确：
  • 衍射孔径比波长大得多
  • 不在太靠近孔径的地方观察衍射场

3.2 从矢量理论到标量理论

• 麦克斯韦方程组
• 介质性质
  • 线性
  • 各向同性
  • 均匀
  • 无色散
  • 磁导率（只考虑非磁性介质）
• 介质满足以上性质时，电场强度和磁场强度的每个分量都满足波动方程：\nabla ^2u = \frac{n^2}{c^2}\frac{\part^2 u}{\part t^2}
• 这就是标量理论的近似过程，类似集总参数

3.3 数学预备知识

3.3.1 亥姆霍兹方程

• P：空间位置；t：时刻
• 纯单色波($\nu$就是相应频率)：$u(P,t)=A(P)cos(2\pi \nu t-\phi(P))=Re(U(P)e^{-j2\pi\nu t})$
  • $U(P)=A(P)e^{j\phi(P)}$就是相矢量
  • 带入波动方程即得亥姆霍兹方程：$(\nabla^2+k^2)U=0$，其中$k=2\pi/\lambda$是波数

3.3.2 格林定理

3.3.3 亥姆霍兹和基尔霍夫的积分定理

• 格林函数$G(P)=\frac{e^{jkr}}{r}$
• 格林函数法（……）
• 亥姆霍兹和基尔霍夫的积分定理：场用边值表示

3.4 平面屏幕衍射的基尔霍夫公式

3.4.1 积分定理应用

• 
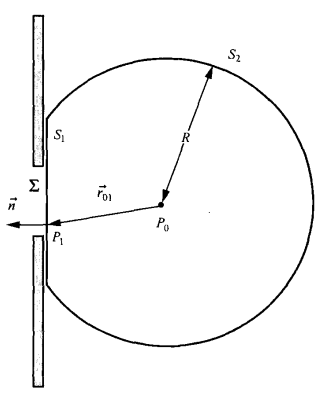
• 直接按几何意义，格林函数$G$在$S_2$上（定向朝外）满足\frac{\part G}{\part n}=\frac{\part G}{\part r}=(jk-1/r)G\approx jkG
• 带入基尔霍夫积分定理，则得索末非辐射条件：\lim_{r\rightarrow \infin}r(\frac{\part u}{\part n}-jku)=0，满足此条件时基尔霍夫积分定理在$S_2$上的积分趋于0

3.4.2 基尔霍夫边界条件

• 假设（后两条为基尔霍夫边界条件，显然是针对u的条件）
  • 满足以上辐射条件
  • 孔径上的场分布及导数和没有屏幕（指挡板）时完全相同
  • 孔径以外的$S_1$的场分布和法方向的导数均为0
• 则基尔霍夫积分定理中的积分区域就是孔径（上图的$\Sigma$）

3.4.3 菲涅尔-基尔霍夫衍射公式

• 两次使用和3.4.1一样的近似，再假设孔径由$P_2$为中心的球面波照明（假设在上图挡板左侧，则$P_1$光场满足此球面波公式），即可通过基尔霍夫积分式得到$P_0$处的光强，带入以上近似即有菲涅尔-基尔霍夫衍射公式
• 亥姆霍兹倒易定理：$P_0$处点光源在$P_2$产生的效果和$P_2$处点光源在$P_0$产生的效果相同

3.5 瑞利-索末非衍射公式

• 基尔霍夫理论的内在矛盾（势函数不可能值和梯度同时为0）——改进：瑞利-索末非理论
• 调整：改G，使其在$S_1$上的值或法方向导数\part G/\part n恒为0，这样我们就不用要求u的场分布和法方向导数均为0
• 第一类：G定义为挡板对称点放相差180°的两个点光源，则$S_1$上G恒为0
  • 于是只用规定U在$S_1-\Sigma$的区域值为0即可（梯度项和G相乘为0，就不用限制了），即可将积分区域限定到$\Sigma$上
• 第二类：……相差为0的两个点光源，则……G法方向导数恒为0
• 两类都是可以的，第一类（常用第一类）导出的结果称为瑞利-索末非衍射公式

3.6 基尔霍夫和瑞利-索末非比较

• 基尔霍夫解是两个瑞利-索末非解的平均
• 瑞利-索末非理论和菲涅尔-基尔霍夫理论的统一形式：倾斜因子

3.7 惠更斯-菲涅尔原理的进一步讨论

• 是次级波的叠加
• 是卷积

3.8 推广到非单色波

• 时间域上可加
• 也可看成次级波叠加，不过根据波长不同，也会有推迟

3.9 边界上的衍射

……

3.10 平面波的角谱

3.10.1 角谱及其物理解释

• 考虑三维空间中平面波（设其方向余弦矢量为$(\alpha,\beta,\gamma)$）在z轴方向的分量，则只需要控制其傅里叶变换的自变量$f_x,f_y$之比为$\alpha/\beta$即可（即设置为$f_x=\alpha/\lambda,f_y=\beta/\lambda$）
• 3.10.2 角谱的传播
  • 当$\alpha^2+\beta^2 < 1$时，不同z坐标的角谱之间只相差一个和$\gamma=\sqrt{1-\alpha^2-\beta^2}$有关的相差，解释为传播延时
  • 当$\alpha^2+\beta^2>1$（正常情况不会出现这种状况），则不同z坐标之间的角谱差一个指数衰减的因子，即这样的波动分量会迅速衰减（称为隐失波），于是在逆变换时（用角谱表示实际光场值时）要乘一个$circ(\sqrt{\alpha^2+\beta^2})$，因为隐失波对值没有贡献

3.10.3 衍射孔径对角谱的效应

• 振幅透射比函数：xoy平面上每一点的透射场振幅比上入射场振幅
• 这个函数（傅里叶变换后）也是透射场角谱和入射场角谱之比
• 当角谱是单位冲击函数（单位振幅垂直照射衍射结构）时，透射角谱就是振幅透射比函数

3.10.4 传播现象作为线性空间滤波器

• 上述传播现象的作用就是线性空间不变系统
• 传递函数是有限空间带宽（需要排除隐失波，和前面的circ是一回事）的线性色散（函数形式和频率有关）空间滤波器