介绍一堆经典的NPC问题,以及证明其为NPC的简要思路。
大量NPC问题
Thm. 归约链
-
SAT 3SAT CLIQUE IS VC SC SubsetSum 另一种SubsetSum
-
SCHS
-
3SATGraph Coloring
注意:这个归约链是可传递的,因此只用证明相邻问题之间可以归约即可。
下面默认归约都指多项式归约,因此省略下标。
归约方法:从多项式时间归约到(),就是构造的实例,变换成的实例,且这个变换只用多项式时间就能完成。如果已知为NPC问题且是NP问题(考试时必须写清是NP问题的证明),则根据NPC问题的定义,也是NPC问题。
但必须注意这里实例之间的变换必须是双射,即的实例应该是一一对应的。(考试时必须写清这种一一对应性,可以先正向后反向地证明)
以下问题中的k值是外部给定的,即问题是是否存在一个k阶解,而非找一个最小/大阶的解(后者非平凡的那个方向通常就不是NPC问题了)。
以下给出证明:
SAT 3SAT CLIQUE
上一节已证。补充一个max CLIQUE问题(MCP问题,即寻找阶数最大的完全子图),这个就是k没给定而求最大阶解的情形,是NP-hard问题。
CLIQUEIS
-
IS:Independent Set problem: 给定一张图G和一个值k,问图中是否存在大小(阶数)为k的独立集。独立集就是顶点之间两两不连边的子图。
- 归约非常简单:取补图即可。显然是多项式时间能够完成的。
ISVC
-
VC:Vertex Cover:给定一张图G和一个值k,问是否存在一个k阶的顶点覆盖
- k阶顶点覆盖:原图中每条边至少有一个顶点在这k个顶点之中
- IS归约到VC的方法:记n为给定图的总顶点数,则给定的IS问题“图G中是否存在阶数为k的独立集”可以归约成“图G中是否存在阶数为n-k的顶点覆盖”的VC问题
- 即如果我们知道VC的n-k阶的解,则取该解相对原图顶点集的k阶补集即为IS,否则n-k阶的解就不是顶点覆盖了(即反证法),反之也类似
VCSC
- SC:Set Cover:给定n阶集合、的m个子集和一个值k,问是否能从m个子集中选出k个使之覆盖原集合
- 归约:给定VC的一个实例,则就定义为图的边集,的m个子集中的第个子集就是VC问题的图中第个顶点所邻接的所有边的集合,这样就可以用解决SC的方法解决VC。这个转换显然是多项式时间能够完成的
SCHS
-
HS:Hitting Set:给定n阶集合、的m个子集和一个值k,问能否取定的一个k阶子集,使得该子集和m个子集中的任意一个的交都非空(所谓“Hitting”)
-
归约方法:给定SC的一个实例,则将其写成一个二维表,描述了各个子集究竟包含了哪些元素(如下图,1/0表示所在行对应的子集包含/不含所在列对应的元素):
-
S\I … 1 0 … 1 1 … … … … … -
然后,把这张表的01部分转置,就可以作为实例交给HS解决了。显然转置是一一且只需多项式时间的。
-
SCSubsetSum
-
SubsetSum:给定整数和,问能否可以选出若干整数使其和恰好为
-
注意:这种整数相关问题的输入规模其实是输入各个整数位数之和,即
-
另外,问题中要求加起来恰好为,不限定的个数(没有指定k),其实和背包问题有紧密联系。
-
首先证明这个问题是NP的(前面的也要证,不过被省略了):
方便起见,引入NP的另一个定义:语言是NP的,当且仅当
- 存在一个能够检查正确性的多项式时间的DTM
- 使得当且仅当
可以接受两个参数,其中是正常的待验证是否在中的串,是一个证书,即对解的一个猜测,或者说假设有对应的NTM能解具这个问题,则可以编码成NTM上运行路径的一个编码。
例如,CLIQUE中一个证书就是任意选择的k个点,此时的任务就是在多项式时间内验证是否是(即)的合法解)
考试时也可用此方法证明NP性,不过要写明的构造方法和验证算法,且二者必须至多多项式复杂度。
- 用这个定义,SubsetSum显然是NP的
-
然后证明NPC:从SC的一个实例((设有n个元素),,k)构造一个SubsetSum的实例
- 首先选一个充分大的进制,如(防止进位)
- 然后设法构建各个(这些都是d进制数)
- 构建方法如下表,下表中第行就是(n位d进制):
-
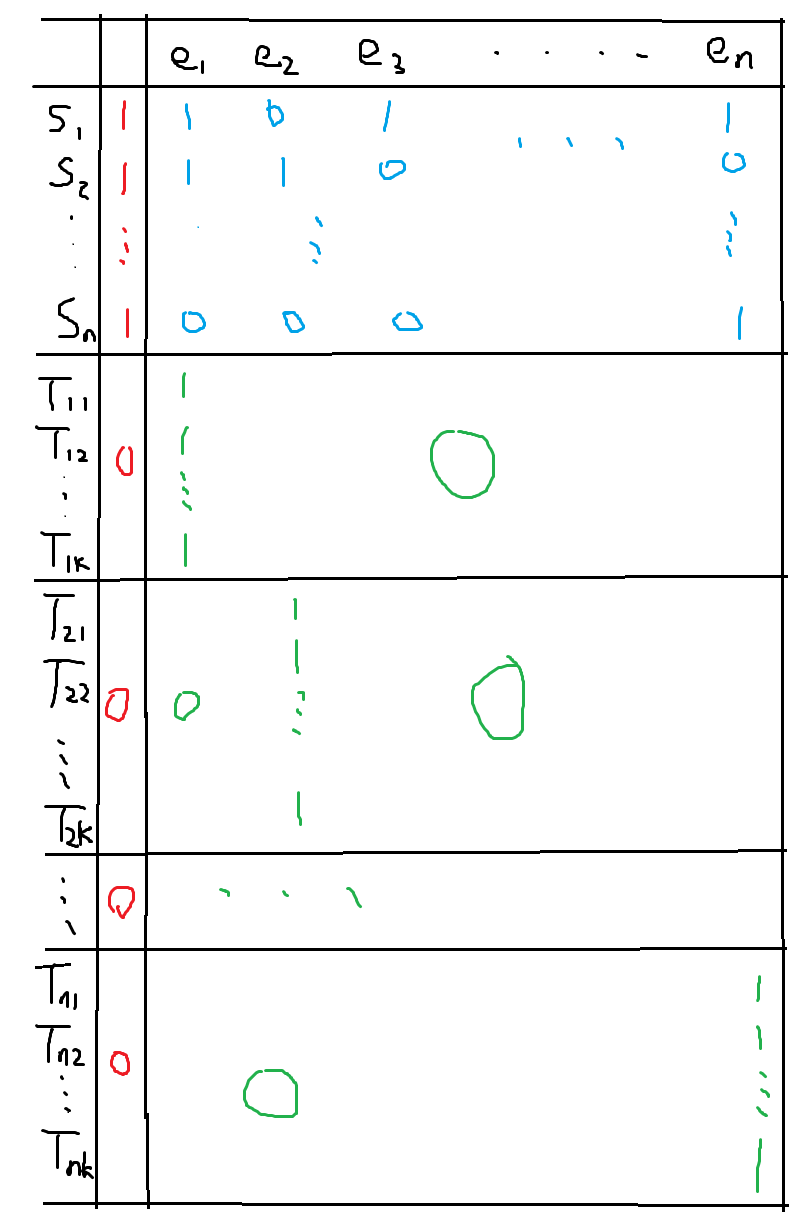
- 其中
- 到是原问题的各个子集,是原问题I的各个元素
- 蓝色部分和HS处的列表规则相同
- 都是添加的辅助变量,具有相同的所有所在行的值都一样,即除从左往右第i位是1,其余n-1位全是0
- 红色部分在所在行为1,在辅助变量行为0
- 最后,我们的选定为(n+1位d进制数,且首位是k,其余每位上的数都是k+1),这就变成了一个SubsetSum的问题。
- 根据d的选取,这里不存在进位,因此根据红色部分,我们的SubsetSum必定会在前n行中恰好选出k个。
- 后面绿色部分每列都只有k个1,想要加到k+1就要求蓝色部分至少有一个1(多了无所谓,可以选择该列为0的辅助变量充数),这和可以覆盖该列所对应的元素等价。后n位每位都是k+1也就等价于覆盖了。
-
SubsetSum另一种SubsetSum
-
SubsetSum的另一种定义:给定整数,问是否可以将这些整数做一个二分割,使得两组的和相等
- 归约:给定原始SubsetSum的实例,则构造时分两种情况讨论(设)
- ,则可以取,若原始SubsetSum有解,则另一种问题可以按照被选中的“k个数”和“其余数”二分割,且和相等;若另一种SubsetSum问题有解,则假设两个分割各自的和为,于是总和是;但,于是,因此原始SubsetSum有解
- ,则可以取,和上面一样。
- 归约:给定原始SubsetSum的实例,则构造时分两种情况讨论(设)
3SATGraph Coloring
-
Graph Coloring
- 给定图G和k,问能否针对顶点进行k染色,使得任意边两端异色
- 2染色(即k=2)可以用BFS搜索是否有奇数长的环解决,有多项式复杂度算法,不是NPC
- G3C就是3染色,k>=3后都是NPC了
- 下面先证明G3C是NPC
- G3C是NP证略(可以用前面NP的新定义,如果给出了一种染色方案的猜想,则显然可以在多项式复杂度内进行验证)
- 下面把3SAT归约到G3C上:给定有n个逻辑变量的3SAT问题,我们按如下方式构造图
- 首先,染色具有轮换性,因此可以先规定三种颜色为0、1、Y且有初始三角形:
-
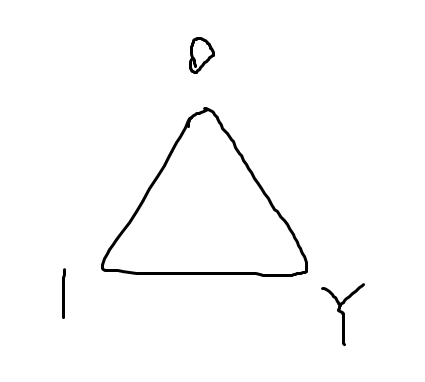
- 然后加约束,第一类:有且只有一个为1,另一个为0(如下图蓝色部分,这里就把所有变量和变量的非都绑定到了某个结点上):
-
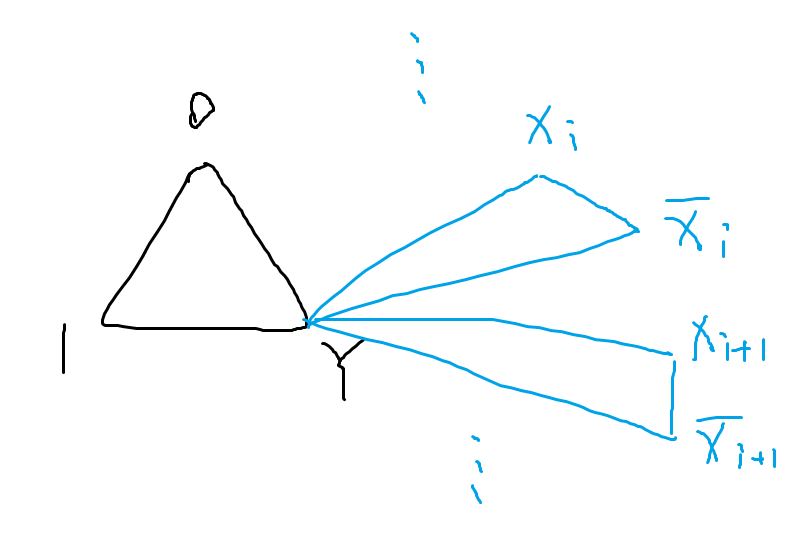
- 第二类:每个子句中三个符号不能都为0。设子句为,则其对应的图可以如下所示构造:
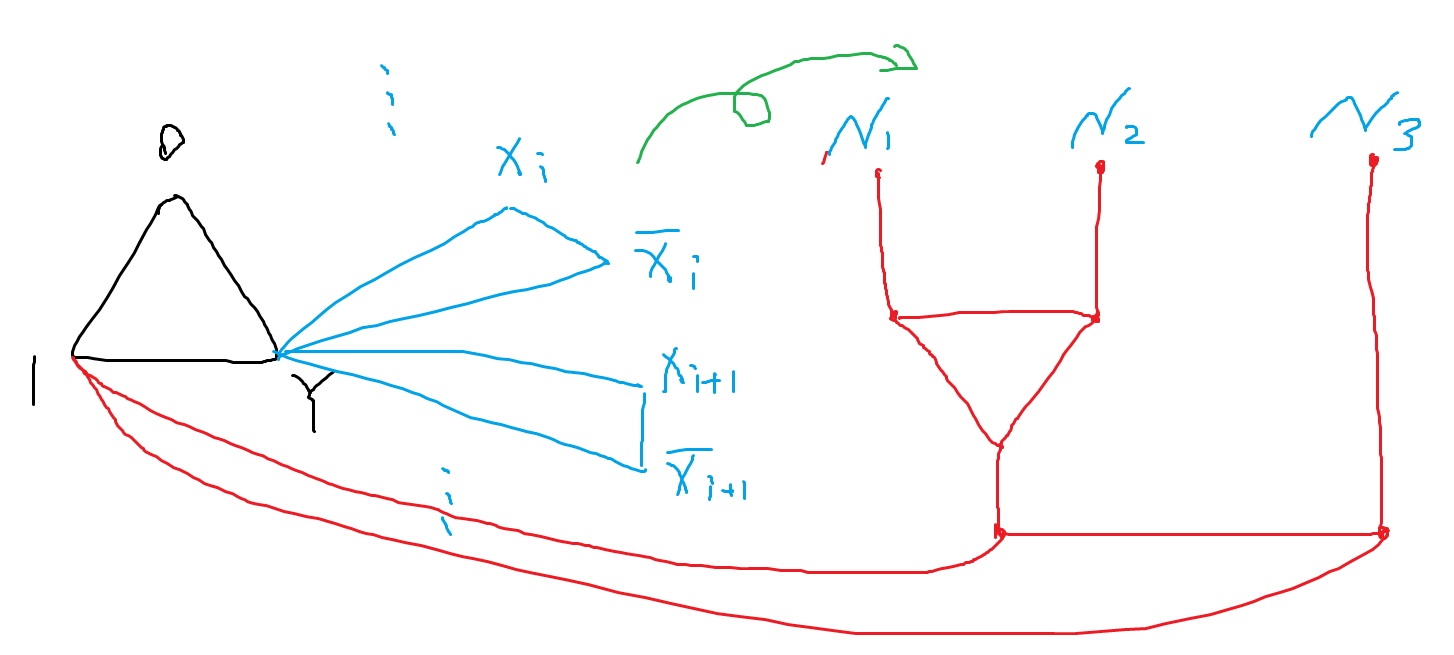
- 于是这张图可否3染色等价于其对应的3SAT逻辑式可否满足
- 然后k>3时GkC也是NPC就很容易证明了
- 假定有G(k-1)C的实例(G,k-1),则可以在多项式时间内将其转换为GkC的实例,方法就是在中加一个和原图中所有结点相连的结点,用GkC染完色后去掉该节点就得到了G(k-1)C的答案,反之亦然。
- 由于已证G3C是NPC,所以这个归约G3CG4C…G(k-1)CGkC…一直成立,于是k>3时的图染色也是NPC