计算理论8

此前讨论的是可计算性，现在则进入有关计算复杂度的讨论。

多项式时间归约

又称Karp Reduction，用新符号 $\le_p$ 标识
仍然可以反映问题的难度。

复杂性

时间、空间、电路复杂度均有定义，这里默认讨论时间复杂度。
$\forall c > 0,DTime(n^c)$ 指用DTM实现，时间复杂度 $O(n^c)$ 的问题（语言）族
反之， $NTime(n^c)$ 指用NTM实现，时间复杂度 $O(n^c)$ 的问题（语言）族
则
- $P=\bigcup_{i=1} DTime(n^i)$
- $NP=\bigcup_{i=1} NTime(n^i)$
我们希望找到某个类中最难的，即类中所有问题都可以划归为这一问题——完全问题（complete）
- 称L是NP-complete若：
  - $L\in NP$
  - $\forall L'=NP,L'\le_p L$ （多项式时间内实现归约）
- 称L是NP-hard若：
  - $\forall L'=NP,L'\le_p L$ （多项式时间内实现归约）
与R、RE的联系：

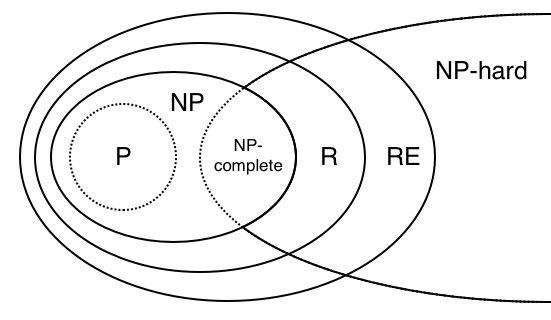
这图是假设P≠NP的情况，若P=NP则P=NP=NPC，三者合成一个圈子。

Cook-Levin Theorem

C-L Thm 存在NPC问题。

证明 SAT问题就是NPC的。

SAT问题的合法串是可满足的逻辑式，即用与或非写出的逻辑式是否能通过对布尔自变量的赋值得到1。
SAT在NP内，因为直接非确定性自动分叉即可同时验证所有赋值的组合。关键是任给NP语言 $L$ ，如何将其划归到SAT上。
假设TM $M = (Q,\Sigma,\delta,q_0,F,\Gamma,B)$ 能够解决 $L$ ，且时间复杂度为 $p=f(n)$ ，其中 $f(n)$ 是关于 $n$ 的多项式（这是因为根据题设， $L$ 是NP问题，可以在多项式时间内解决）
对任意 $w\ (n=|w|)$ ，我们下面借助SAT构造相应的TM来模拟 $M$ 的运行，从而实现 $L$ 到SAT的归约
- 首先，新TM的纸带字符为 $M$ 的ID。由于 $L$ 时间复杂度是 $p$ ，则 $M$ 指针左右移动的最大范围都是 $p$ 。因此可以取一个松一点的上界：每个ID对齐后的长度（字符数）也不会超过 $2p+n+1$ 。同样由于复杂度为 $p$ ，因此新TM至多运行产生 $p$ 个ID后就会到达终止态。
- 于是，我们可以把新TM的纸带“竖”着展开，变成一个二维表格，表格中的每个格子都可以填入 $Q\cup \Gamma$ 中的某个元素，每行是一个ID。于是这个表格就是 $p$ 行 $2p+n+1$ 列的，如下图是 $w=abc$ 的示例：
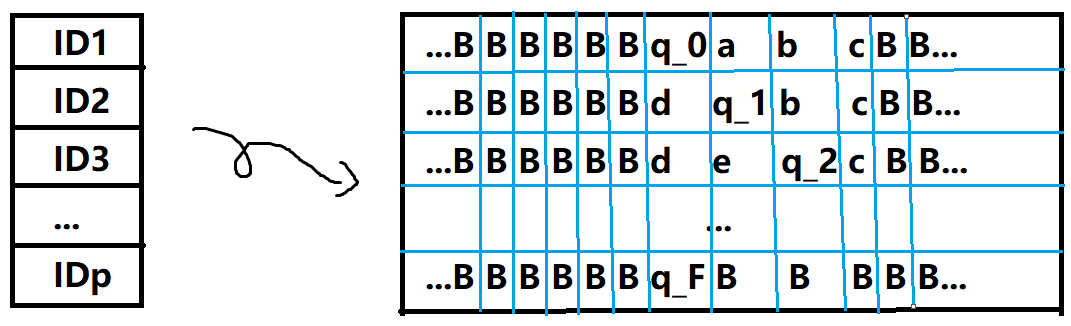
- 如果ID数量没到 $p$ ，则把停机时带 $q_F$ 的那个ID向下复制即可。
- 随后我们将这张表转换为布尔变量，并将这张表需要受到的约束写出来：每个布尔变量都有三个下标，第一个下标索引第几个ID，第二个下标索引该ID中的第几个字符，第三个下标索引纸带字符集和状态集之并中的一个元素。
- 若该ID该字符处就是第三个下标的元素则该变量为1，否则为0——于是总共有 $p\times (2p+n+1)\times |Q\cup\Gamma|$ 个布尔变量
然后构造逻辑式，使得逻辑式为1当且仅当这张表格表述的ID序列推导过程（根据 $M$ 的转移函数）合法。这个逻辑式由四个约束相与构成：
1. 第一行必须包含起始态；
2. 每格有且只有一个符号，即每个格子对应的 $|Q\cup\Gamma|$ 个变量中有且只有一个为1；
3. 最后一行必须包含终结态
4. 相邻两行之间满足转移函数的约束关系：
  - 两行之间只要三个三个元素地比较即可（如下图），即每次只用看二行三列的范围内是否合法即可，每两次判断之间都有一个2*2的重合范围
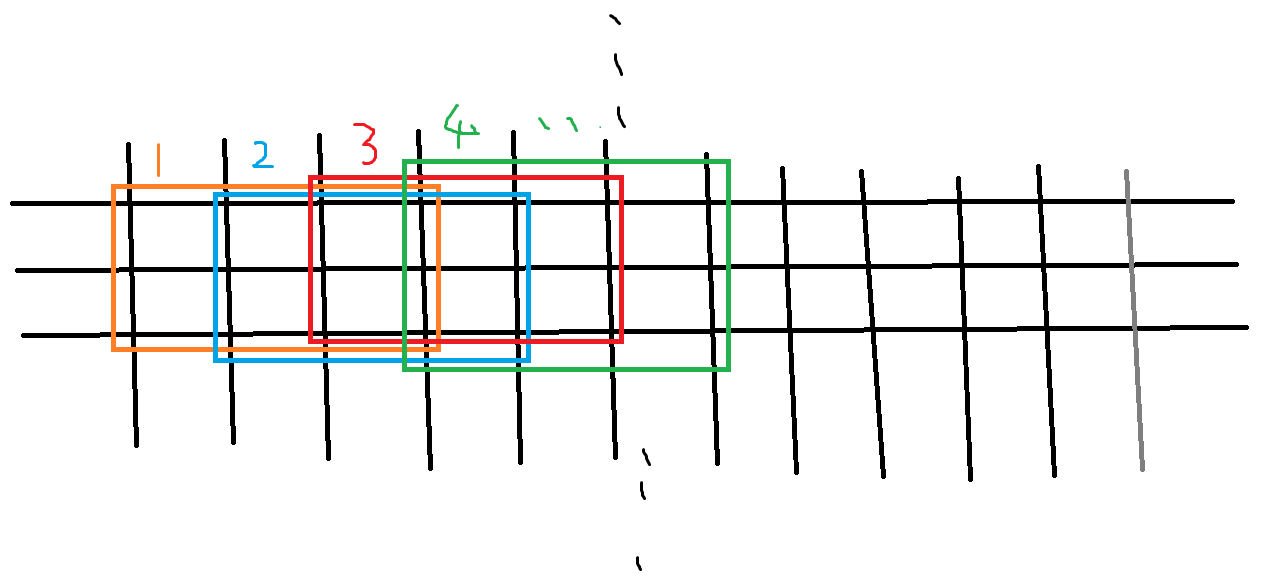
  - 这个地方没有简洁的方法，只能逐个列举所有合法的情形。注意：只要行与行之间合法，就不用担心一行有两个状态之类的情况。
  - 如果遇到终结态就忽略，直接合法
所有四个东西合在一起就是我们需要的逻辑式，然后扔给能解决SAT的TM，若SAT接受则表示有合法的转移路径，因此 $w$ 应该被接受
这就是一个instance-level的归约，且只需要多项式时间（只用填表），因此SAT就是一个NPC问题

3SAT

和SAT问题相似，但逻辑式 $\phi$ $ϕ$ 有特定格式：
- $\phi = C_1\land C_2\land ...\land C_n$
- 其中 $C_i$ 为 $N_k\vee N_l\vee N_m$ （三元形式的子句）
- $N_k=X_k$ 或 $N_k=\bar{X_k}$ ， $X_k$ 就是真正的变量
3SAT也是NPC

SAT可以多项式时间归约到3SAT

根据逻辑式长度作归纳法即可，但非常小心这里的逻辑式是变量！！！(因此归纳时必须强调变量并加变量)
我们先设计转为合取范式的多项式时间算法，然后设计满足3SAT要求的多项式时间算法。我们可以分别考虑按照 $\land$ 或 $\vee$ 分割逻辑式的情况
假设比 $\phi=\phi_1\land\phi_2$ 更短的逻辑式都能转成可满足的合取范式（于是 $\phi_1,\phi_2$ 都能如此转换），且 $\phi_1,\phi_2$ 在可满足时对变量值的要求是不矛盾的

注意：这里必须加强归纳假设，如果归纳假设仅仅是比 $\phi=\phi_1\land\phi_2$ 更短的逻辑式都能转成 $3SAT$ ，则 $\phi_1\rightarrow \psi_1,\phi_2\rightarrow \psi_2$ ， $\psi_1,\psi_2$ 都是满足3SAT格式要求的逻辑式且都在 $\phi_1,\phi_2$ 均可满足时可满足，但 $\psi_1\land\psi_2$ 就未必可满足了，因为二者对变量值的要求可能起冲突（例如满足 $\psi_1$ 需要 $X_1=1$ ，而满足 $\psi_2$ 需要 $X_1=0$ 之类）

则很显然 $\phi$ 也是一个可满足的合取范式。
假设 $\phi=\phi_1\vee\phi_2$ 更短的逻辑式都能转成可满足的合取范式，则我们先把 $\phi_1,\phi_2$ 转成可满足的合取范式 $\psi_1,\psi_2$ ，然后新增辅助逻辑变量 $y$ ，在 $\psi_1$ 的每个子句中添加 $\vee y$ ，在 $\psi_2$ 的每个子句中添加 $\vee \bar{y}$ ，则 $\psi_1 \land \psi_2$ 就是我们需要的可满足的合取范式。
最后把合取范式转为3SAT的形式，还是通过添加辅助逻辑变量 $y$ 的方式完成。

示例： $C_i=N_1\vee N_2\vee N_3\vee N_4$ ，添加 $y$ 之后可以拆成 $(N_1\vee N_2\vee y)\land (N_3\vee N_4\vee \bar{y})$ ，如果拆短了（子句只有两个变量）可以直接复写其中一个变量或是添加一个其他地方没出现过的变量将长度补到3。
证毕

注：

2SAT就有多项式时间算法了

实际做题归约到3SAT通常是最方便的

CLIQUE

CLIQUE：给定一个图，再输入一个k，问这个图中有无k阶完全子图。

注意：必须是输入一个 $k$ ，不然若 $k$ 是定常值则很容易给出暴力多项式算法。
可以证明3SAT $\le_q$ CLIQUE：
假定有TM $M$ 能够解决CLIQUE问题，则我们可以把3SAT转化为一个CLIQUE问题的输入（即变成一个图）：
- 假定3SAT有k个子句，则新图中就有3k个结点，结点按照“在同一个子句中”分成k个三点组，每个组之间都不连边；组与组之间除了 $X_k$ 和 $\bar{X_k}$ 这种矛盾的结点不连边以外，全都连上边。
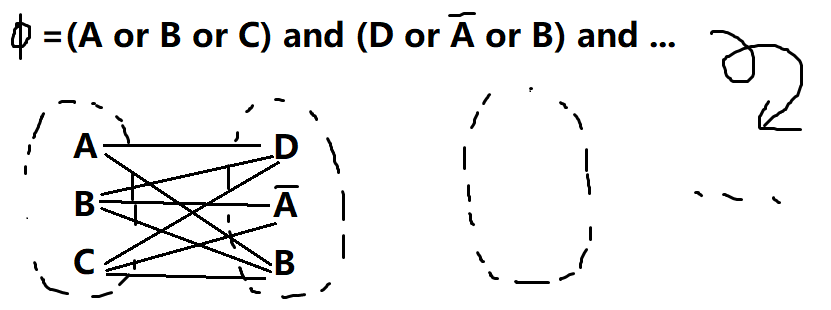
- 此时，原逻辑式可满足当且仅当该图中有k阶完全图
  - 由于同组不连边，则该完全子图必然是每组选出一个结点
  - 能满足的赋值方法就是把选到的节点赋值为1即可
  - 反之，把能满足逻辑式的赋值方法中被赋值为1的结点选出来必然会形成k阶完全子图

不重要的注记：Hexo笔者当前配置的渲染器是KATEX，部分公式和LATEX有少量区别，参见https://katex.org/docs/supported.html。Typora貌似可以同时渲染两种版本的数学公式，需要在部署前仔细检查。