计算理论7

介绍和图灵机计算能力以及相应的语言层次结构、可判定性等内容。

NTM与DTM的计算能力

• 二者的计算能力相同
• 但二者的计算效率（复杂度）不同

多带图灵机（Multi-tape TM）

• 多个指针多个纸带，还是只有一个控制器
• 若有k条纸带，则控制器为DFA时的转移函数定义为$\delta:Q\times \Gamma^k\rightarrow Q\times \Gamma^k \times \{\rightarrow,\leftarrow\}^k$
• 初始ID：第一条纸带有输入，指针指到起始字符；其余纸带为空

计算能力

Thm k-tape的TM和1-tape的TM计算能力相同（以下只证$k=2$的情况，$k>2$的情形可以类似地证明）

• 只用证一个方向就行：$\forall L,\exist$ 2-tape TM $M$使得$L(M)=L$，则是否$\exist$ 1-tape TM $\widetilde{M}$使得$L(\widetilde{M})=L$
• 类似证明正则语言对交的封闭性，可以考虑把两条纸带“乘”（笛卡尔积）起来，即新纸带的字符集是$\Gamma \times \Gamma$
• 但这里还有个指针问题，比如两条tape的指针可能一个向左走，一个向右走，这就没法像DFA一样处理了
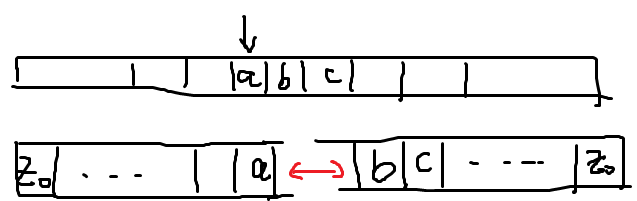
• 因此新纸带的每个字符其实应该是四元组，字符集为$\Gamma\times\{p,B\}\times\Gamma\times\{p,B\}$，其中$p$代表“指针在此处”，整条新纸带的第2、4号位（即下表的第2、4行）除表示原2-tape TM纸带位置的$p$以外，其他地方都是B
  • 示例如下：前两行（对应四元组的前两个元素）表示第一条纸带的内容和第一条纸带当前指针的位置（用p标示），后两行则相应表示第二条纸带的情况

……	a	b	c		……
……	p				……
……	d	e	f	g	……
……			p		……

• 规定新DTM的指针指向2-tape情形下靠左的指针（如上图中指向第二行p的位置），则新DTM可以模拟2-tape的工作情况：
  • 首先读到其中一条带子上的当前字符
  • 然后向右找到另一条带子的当前字符，据此即可确定下一步的状态、字符、指针变化（参见转移函数$\delta$的定义）
  • 先改另一条带子的当前字符，再移动靠右的$p$，再一直向左找到靠左的指针，改变对应字符，最后改变靠左的$p$的位置

计算效率（复杂性）

Thm 存在语言L，使得1-tape的复杂度是2-tape的平方量级

• 一个例子是$L=\{ww|w\in \{0,1\}^*\}$
• 可以证明：单带识别此语言的复杂度下限为$O(n^2)$（一种识别方法在前面已经列出）
• 双带则可以拷贝待判定串的前一半到另一条带子上，然后逐位比较（注意两条带子的指针可以指向不同的位置），则只用$O(n)$

Thm 不存在语言L，使得1-tape的最优复杂度比2-tape的最优复杂度的平方量级还高

• 证明方法和“计算能力”部分的证明相同，设2-tape下复杂度为$O(T)$
• 用1-tape模拟2-tape上$O(1)$的一次操作的复杂度不会超过$O(T)$，因为2-tape上$O(T)$次操作后两个指针之间的间距不会超过$O(T)$量级（不妨假设开机时两条带子指向同一个位置）
• 因此1-tape的复杂度为$O(T)\cdot O(T)=O(T^2)$

带数$k>2$时，用1-tape模拟的复杂度也不会超过k-tape的平方量级，因为k-tape时的k个指针中离得最远的两个之间的距离也不会超过$O(T)$。因此从渐进复杂度角度而言2-tape后再加纸带是没用的。

双栈PDA

• 双栈PDA不能被单栈PDA模拟，因为双栈PDA和TM计算能力等价
  • 一方面，栈的计算能力不会比纸带强，因此双栈可以被2-tape模拟，而1-tape和2-tape等价，因此双栈PDA的计算能力上限不会超过TM
  • 另一方面，双栈可以模拟TM：类似双栈成队，但是是把栈顶给“粘”起来，TM的指针移动就是其中一个栈pop，改写一下元素，然后push到另一个栈中
  • 
  • 当然还有一步：PDA读入串时需要先逐个压入栈，然后再把所有字符pop-push到另一个栈中从而变成倒序状态，就能模拟TM的初始状态了
• 进一步的计算模型：Counter Machine，即是双栈PDA，但栈字符只有$Z_0$和$X$（即有效的栈字符只有一个）。此时相当于只能判断栈是否为空。但可以证明Counter Machine和TM等价

NTM和DTM的等价性

• 只用考虑如何构造DTM来模拟NTM
• 根据前面的讨论，可以选择构造多带的DTM
• 考虑ID
  • 初始$ID_0=q_0w$
  • DTM的ID转移构成一个路径，而NTM的ID转移构成一张有向图（转移路径上完全有可能有环，因此不是多叉树）
  • 关键是有向图可能是无限延展的，也可能有环（即可能不停机），因此不能在ID上进行DFS，只能BFS，于是复杂度必然指数增长了。但是否有比指数增长更快的办法尚无定论。
• 构造：用2-tape，模拟“内存”和“外存”进行BFS
  • 纸带的字符为ID
  • 把初始ID写到带1上
  • 随后BFS，每从带1上读到一个ID就将其复制到带2上并擦除带1上该ID的内容
  • 然后解析刚刚读到的ID能够到达哪些ID，并将这些ID挨个“续写“到带1非空白部分最右端的空白部分
  • 下一步就取带1上非空白部分最左边的ID，循环执行
• 上面这种方法模拟NTM其实就是BFS，因此需要额外花费指数级的复杂度

TM计算能力上限、语言层级

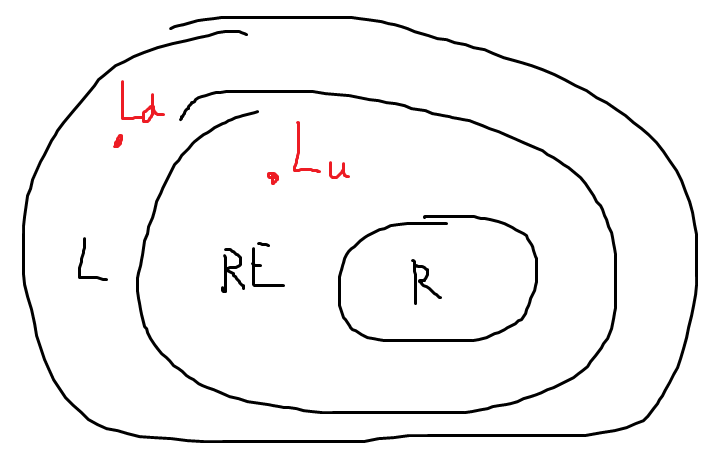
• TM能计算的语言就是递归可枚举语言（Recursively Enumerable，RE），即$\{L|\exist TM\space M,L=L(M)\}$

• 举例：丢番图方程的解。

  • 能否定义一个RE语言包含所有有非平凡解的丢番图方程（所对应的多项式）？
  • 答案：可以，直接构建$n+k$个纸带的TM，其中$n$表示待讨论的丢番图方程的变量个数，$k$条纸带可以用来计算
  • 然后我们在$n$条纸带上枚举各个变量的取值，但枚举顺序不能DFS，需要使用BFS（比如根据$n$个变量的和为1，2，3，……的顺序来枚举）
  • 注意！这样构造出来的图灵机可计算的语言恰好就是这个语言！因为如果有解则必然会被接收，无解虽然会永远执行下去（不停机），但不停机也是不接收（可以看看前面TM”接收“的定义）。这就是”递归可枚举“的含义。

• 因此递归语言（Recursively，R）更有实际意义：即$\{L|\exist TM\space M,L=L(M)\}$且**$M$必须在任何输入下都能停机**

  • 注意：无论R还是RE都是“存在图灵机$M$使得……”即可，因此这是语言的特征而非某台TM的特征

• 递归可识别语言RE称为TM可识别，递归语言R称为TM可判定

• 所有语言的集合L，递归可识别语言RE，递归语言R是一个真子集链的关系，如下所示（随后给出证明，$L_d,L_u$稍后出场）：

  

$RE\subsetneqq L$

• Counting Argument：八个苹果放到九个盒子里，则至少有一个空盒子
• 因此只要证明语言总数比RE总数"多"即可（当然，后面也会具体给出一个实例）
• 复习：对无穷集合而言，这就是比较二者的基数（势）
  • 等势：能构造双射
  • 若能构造$A\rightarrow B$的单射，则$|A|\le |B|$。
• 下面将证明$|RE|=\aleph_0 < |L| = \aleph_1$。注意这里$L$表示所有语言的集合
• 复习：首先证明存在不可数（不可列）的集合
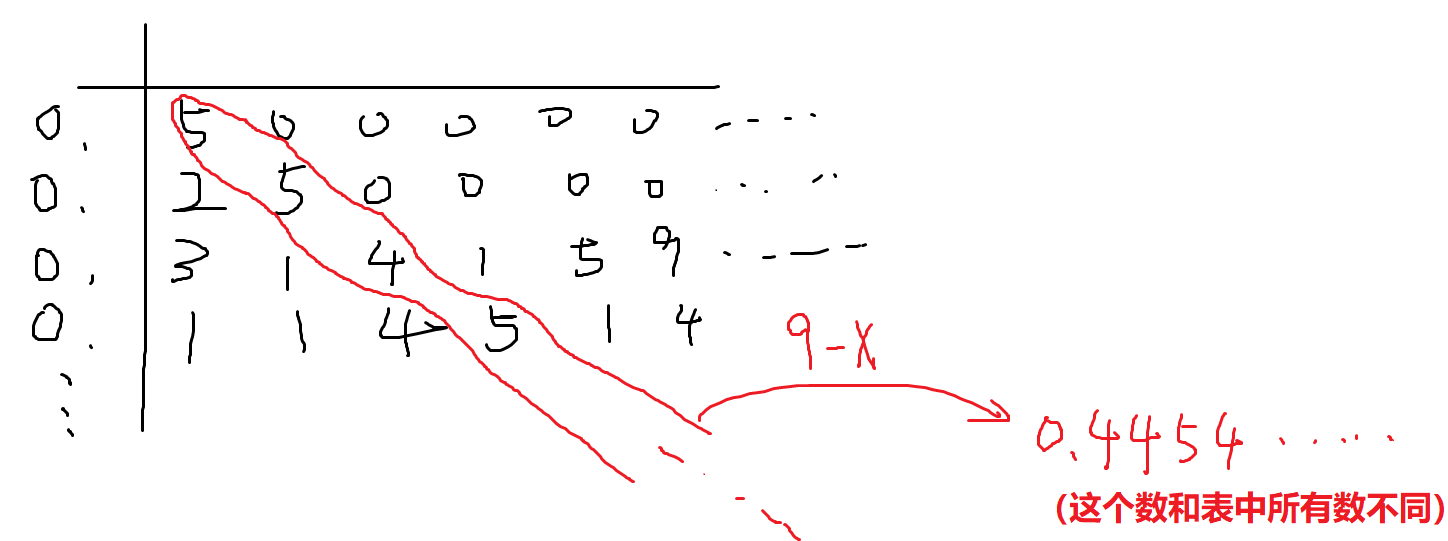
  • 示例：$(0,1)$之间的实数，证明就用康托的对角线法则
  • 假设这些小数按某种方式一一全部填入一张表格，若是有理数则把后缀的0全部补上，于是变成二维数表
  • 然后取对角线的一串数字构造一个$(0,1)$之间的小数，就能得到一个不在这张表的小数，矛盾
  • 示例：
  • 
• $|L|=\aleph_1$：简便起见，令字符集为$\{0,1\}$，于是任何一个基于此字符集构造的串都能和二进制下的一个正整数一一对应，因此$|\{0,1\}^*|=\aleph_0$。由于每种语言都是$\{0,1\}^*$的一个子集，因此$|L|=|2^{\{0,1\}^*}|=\aleph_1$
• $|RE|=\aleph_0$：我们需要按照这些规则对图灵机进行修改：$q_1$是起始态，$q_2$是唯一的终止态（若有多个终止态，就加一个“真正的终止态”，所有的终止态无条件转移到这个真终止态上停机即可），剩下的状态是$q_3,...,q_s$；纸带字符集$\{a_1,a_2,...,a_t\}$中的$a_1=B$
  • 则转移函数$\delta(q_i,a_j)=(q_k,a_l,direction)$，其中$direction\in \{\leftarrow, \rightarrow\}$
  • 我们可以构造一个转移函数到01串的一一映射：
    • $1^i001^j001^k001^l00\{1,11\}$，$\{1,11\}$表示根据$direction$选择填1或11。这里的$00$存粹起的是分隔符的作用
    • 某个图灵机的转移函数的每一条映射都按如上方式转换，再按照大小排序（这是为了保证转移函数到这种01串是一一对应的）用四个0（$0^4$）作为分隔符连接起来；图灵机其余部分很容易类似编码，
    • 于是每台图灵机都可以编码成一个01构成的整数
  • 因此所有图灵机组成的集合的基数不超过$\aleph_0$，由于每个RE中的语言都需要存在TM来实现它，因此由所有RE语言组成的集合的基数也不会超过$\aleph_0$

第二种证明思路：直接举出一种语言$L_d$，使$L_d\notin RE$

• $L_d=\{w_M|w_M\in \{0,1\}^*,w_M\notin L(M)\}$，其中$M$代表图灵机，$w_M$表示$M$对应的01编码（编码方式见前）
  • 即$L_d$是由不能计算自己的图灵机的01编码组成的语言
  • 这个定义涉及自我指涉，其实有奇异的风险。但可以证明这确实是一个ZFC公理体系下的集合（证略）。
• 于是可以用类似Russell悖论的方式导出矛盾：假设$\exist M', L(M')=L_d$，则问$w_{M'}$是否在$L_d$中？
  • 若$w_{M'}\in L_d=L(M')$，则$w_{M'}\notin L(M')$，矛盾；反之，若$w_{M'}\notin L_d$，则还是矛盾

$R\subsetneqq RE$

• 构造反例：$L_u=\{w_M0^6x|x\in L(M)\}$（下标u表示universal）。即这台图灵机可以运行其他所有图灵机（把待判定输入和其他图灵机对应的01编码拼起来输入这台图灵机就行）

  技术性的注解：$0^6$其实只是一个分割符，只是为了和前面的$0^2$，$0^4$两种分割符相区别，改成别的也可以

• 首先需要说明$L_u\in RE$，大体思路其实就是把$L_u$对应的图灵机按照编译器的路子来写就行了（$w_M$就是我们写的程序，$L_u$对应的图灵机先把$w_M$解码翻译成$M$，然后模拟运行即可）

• 定理 $L\in RE$且$\bar{L}\in RE$当且仅当$L\in R$。

  • 注：这里的$L$指某个特定的语言，和前面的含义又不一样了
  • 正向证明：因为存在$M_1$能让$L$能接收的语句停机，存在$M_2$能让$\bar{L}$能接收的语言停机
  • 这两个图灵机虽然不一定一样，但我们可以构造一个多带的图灵机，“交替”执行$M_1$和$M_2$，即一个TM走一步，下次就是另一个TM走一步（BFS），这样必然会停机。输出部分修正一下，这个新的多带TM就能处理$L$且必定停机了
  • 反方向根据定义即证

• 考虑$\bar{L_u}=\{w_M0^6x|x\notin L(M)\}$，假设它在RE内

  • 能计算$\bar{L_u}$的图灵机$M'$必然能计算$L_d$，因为向$M'$输入$w_M0^6w_M$，若在$w_M\in L_d$则必然能停机并给出接收的判断（因为假设了$\bar{L_u}$是RE）
  • 这和$L_d$不是RE矛盾！
  • 因此$\bar{L_u}$不是RE，根据定理可知$L_u$不是R（或者也可以说因为$L_u$可能无法在负例下停机，因此不是R）

可判定性的判定与实例

停机问题

• 可以形式化为对语言的讨论（有两种版本）：

  • 第一种：$L_h = \{w_M0^6x|M\space halt\space with\space x\}$

  • 第二种：$L_h = \{w_M|M\space halt\space with\space \epsilon\}$

Thm 这两种语言都是图灵可识别（RE）但不可判定（非R）的

证明 以第一种为例：

归约法（Reductions）：设有语言$A$、$B$，欲证$A\le B$（即$A$的“难度”不超过$B$，比如$A$如果不是RE则$B$也不是RE），则只要能解决$B$的图灵机$M$也能（在一定的调整后）解决$A$（把$A$问题变成$B$问题）即可。

另重新将常见用于归约的中间语言列下：

$L_d=\{w_M|w_M\notin L(M)\}$（不是RE）

$L_u=\{w_M0^6x|x\in L(M)\}$（所谓“万能图灵机”，是RE但不是R）

• 正向：假定$\widetilde{M}$能解决$L_u$，则该图灵机必然能解决$L_h$
  • 因为直接把$w_M0^6x$塞进$\widetilde{M}$，则$\widetilde{M}$能输出结果（无论接收还是拒绝）都当且仅当$w_M0^6x\in L_h$（$\widetilde{M}$就是按照模拟的方式进行工作的），这保证了在$L_h$中的串都能被接收。
  • 因此$L_h$难度不会超过$L_u$，即$L_h$至多是RE的
• 反向：假定存在$\widetilde{M}$能解决$L_h$且都能停机（即假设$L_h$是R）
  • 则我们就能构造一个新的图灵机$\widetilde{\widetilde{W}}$解决$L_d$:
• 
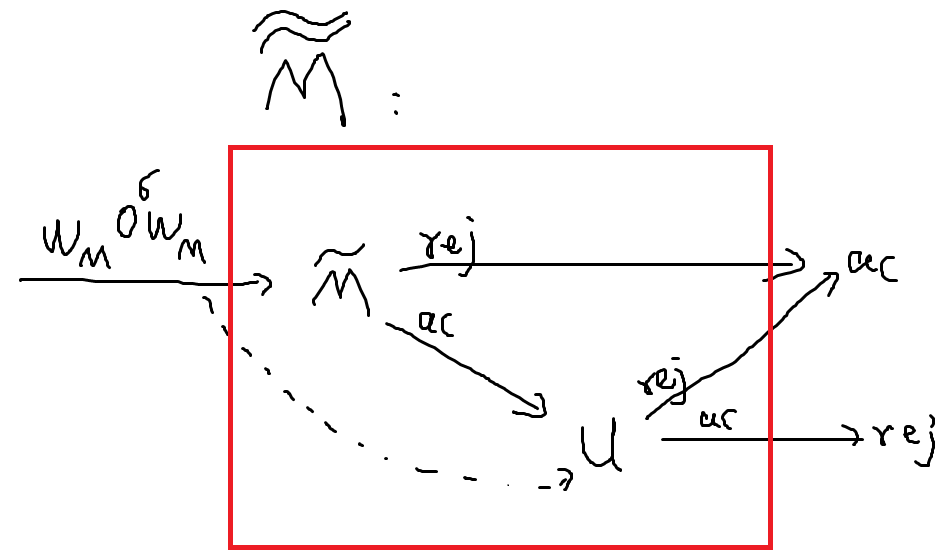
  • 这个构造的原理是：首先由$\widetilde{M}$对输入进行判断，看$M$输入$w_M$时是否会停机。
  • 注意$\widetilde{M}$本身根据假设是不会停机的，因此上面的过程总是会在有限时间内在两种答案中二选一：会停机（ac）、不停机（rej）
  • 若是不停机则表示$w_M$压根不会被$M$接收，因此最终输出为接收（即$w_M\in L_d$）
  • 若是停机，则找一台能识别$L_u$的“万能”图灵机$U$，然后把$w_M0^6w_M$塞进去。由于已经验证过必定会停机，因此$U$必然会在有限时间内输出接收或不接受。接收则最终输出不接受，不接受则最终输出接收，这样就把$L_d$实现了。
  • 然而前面已证$L_d$不是RE的，因此矛盾，$L_h$不是R！

空语言/非空语言

• $L_{ne}=\{w_M|L(M)\ne \empty\}$是递归可识别（RE）但不可判定语言（R）

  • 对应TM构造方式：用万能图灵机$U$逐串进行验证，串的枚举顺序按照“串长+已运行步数（为防止某些串不停机）”排列即可，故为RE
  • 然后说明能实现$L_{ne}$的TM都能实现$L_u$。
    • 考虑输入串$w_M0^6x$，我们需要造一台新的TM$M'$，使得$x\in L(M)$当且仅当$L(M')\ne \empty$。造好之后把$M'$的编码$w_{M'}$塞进$L_{ne}$，就能实现$L_u$了。
    • 实现方式就是$M'$根本不管输入，而是直接用$w_M0^6x$把纸带原本的内容全部覆盖掉，再调用能实现$L_u$的TM看$x\in M$是否成立，并以此作为$M'$的输出。于是$x\in M$时$M'$接收任何串，反之则不接受任何串，符合前面的要求。

• 于是$L_e=\{w_M|L(M)=\empty\}$根据前面的引理不可识别（非RE）

  • 假设$L_e$是RE的，则由于$L_{ne}=\bar{L_e}$也是RE的（已证），于是二者都是R的，这和$L_{ne}$不是R的相矛盾。

• 同理，$\bar{L_h}$（不停机问题）是不可识别的（非RE），因为$L_h$是RE且非R的。

• $L=\{w_M|000\in L(M)\}$可以用万能图灵机（是RE）模拟，因此是可识别的（是RE）；但可以证明$\bar{L}$是不可识别的（结合Rice定理很容易看出$L$不可判定，从而仿照上面的证明可以看出这一点）。

Rice定理

Thm $\forall P\sub RE$（即以任意性质挑出有一定特征的RE语言组成集合）且$P$非平凡，则语言$\{w_M|L(M)\in P\}$总是不可判定（非R）的

• 注意：$P$必须是非平凡的，即不能是全集或空集。

• 通俗化理解：判定可判定语言是否具有某种非平凡性质的问题都是不可判定的。但这种问题有可能是可识别的（RE）。（此时可以借助Rice定理和前面已证明的定理“$L,\bar{L}\in RE\rightarrow L,\bar{L}\in R$”反证出其补语言是不可识别的。）

• Rice定理有意思的推论：以下问题都是不可判定的（当然，这些语言的不可判定性未必必须使用Rice定理才能证明）：

  • 某图灵机能接收的语言是否为空/是否非空（即前面讲的空语言/非空语言）；
  • 某图灵机能接收的语言是否有限；
  • 某图灵机能接收的语言是否是正则/上下文无关的；
  • ……

• 必须是针对可判定语言的性质，而非是针对图灵机的性质，这一点需要小心分辨。

  参考https://courses.engr.illinois.edu/cs374/fa2015/slides/Undecidability-Rice.pdf

  • 针对图灵机的性质的示例（以下问题不能套用Rice定理）：
    • $\{w_M|M\ has\ 100\ states\}$
    • $\{A.cpp|program\ A\ has\ 100\ lines\}$
    • 停机问题
  • 针对图灵机的性质的问题有的可判定，有的不可判定。上面三个例子中的前两个就是可判定的，最后一个停机问题就是不可判定的。
  • 但是并不是在“性质”的描述中出现图灵机就是在针对图灵机的性质，如$\{w_M|000\in L(M)\}$就可以套用Rice定理（这种描述实质上还是针对语言的性质）

• 证明仍然是借助$L_d,L_u,L_h$的性质，略

  注意：停机问题其实和Rice定理是等价的（https://arbital.com/p/rice_theorem/?l=5n6）。尽管停机问题不能直接套用Rice定理，但还是可以间接地用到Rice定理进行证明。不过停机问题的不可判定性可以不借助Rice定理直接证明（见前），因此一般是用停机问题去证明Rice定理。

PCP的不可判定性

• Poster‘s Correspondence Problem（PCP）的定义：

  • 由$(\Sigma,A,B)$组成

  • $A=w_1,...,w_k;B=x_1,...,x_k$是两个有限且串数相同的字符串表

  • $\Sigma$就是以上两个串表的字符集

  • 下标相同的一对串$(w_i,x_i)$称为对应对（Corresponding pair）（通俗说法就是一张牌，见后）

  • 称一个PCP问题有解，当存在一组序数$i_1,...,i_m$（可重复使用，但不允许$m=0$），使得$w_{i_1}w_{i_2}...w_{i_m}=x_{i_1}x_{i_2}...x_{i_m}$

  通俗解释：现有一组扑克牌（牌种类数有限），每张牌分上下两部分，每部分任写一个串，每张牌可以复制无限份（用无限多次），问能否取出若干（有限）张牌，使得上部分连缀起来的串和下部分连起来的串相同？

  示例：

  

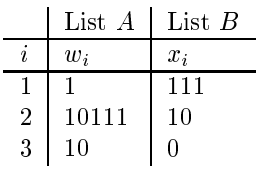
  则这个PCP问题有解，如2，1，1，3（见下）

  	2	1	1	3
  w	10111	1	1	10
  x	10	111	111	0

  但也存在PCP无解。

定理 “PCP是否有解”是可识别（RE）但不可判定（非R）的。

• 可识别：枚举各种牌的组合，按照组出的两个串的总长度由小到大顺次枚举即可，于是是RE

• 不可判定性的证明：先将MPCP问题归约到PCP问题上

  • MPCP问题：其他要求和PCP相同，但第一张牌必须使用指定的一张牌，即有解条件变为当存在一组序数$i_1,...,i_m$（可重复使用，且允许$m=0$），使得$w_1w_{i_1}w_{i_2}...w_{i_m}=x_1x_{i_1}x_{i_2}...x_{i_m}$
  • 定理 MPCP可以归约为PCP问题（证略）
  • 于是，若MPCP不可判定，则PCP也不可判定。

• 随后将$L_u$问题归约MPCP到上

  这里的归约是一个instance-level的归约，即$L_u$的输入经过一个映射可以得到MPCP的一个输入。前面的Turing机的归约则是构造使用了较难问题图灵机的一个新图灵机。

  • 即给定$w_M0^6x$，我们可以构造出相应的$\Sigma,A,B$，使得$M$接受$x$当且仅当$(\Sigma,A,B)$这个MPCP问题有解。
  • 关键在$\Sigma$，这里我们定义用来组成TM的ID的字符为字符，再定义一个分隔符$\#$（当然，根据编码方式不同也可以有别的方法，例如此前用特定数量的0做分隔符。这里方便起见，还是用$\#$好了）
  • 再构造$A,B$，使得寻找MPCP问题是否有解的过程中，$w_1w_{i_1}w_{i_2}...$和$x_1x_{i_1}x_{i_2}...$都增长，且后者比前者长出一个ID，直到到达接受态为止。

  1. “第一张牌”：

     A	B
     $\#$	$\#q_0x\#$

     即从第一张牌开始$B$组出的串就比$A$的串多一个ID。注意这是MPCP，因此必须从这张牌开始执行（这就是使用MPCP而非PCP作证明的方便之处）。

  2. 基础字符可任意添加：

     A	B
     $X$	$X$ (for each X in $\Gamma$ of $M$)
     $\#$	$\#$

     其中$X$是给定的图灵机$M$的纸带的字符集中的任意一个字符。

  3. 模拟转移函数

     A	B	对应转移函数
     $qX$	$Yp$	$\delta(q,X)=(p,Y,\rightarrow)$
     $ZqX$	$pZY$	$\delta(q,X)=(p,Y,\leftarrow)$
     $q\#$	$Yp\#$	$\delta(q,B)=(p,Y,\rightarrow)$
     $Zq\#$	$pZY\#$	$\delta(q,B)=(p,Y,\leftarrow)$

     当然这只是一种简化的构造（见p407）——总之，我们试图让ID中不用出现空字符$B$。$Z$是任意一个纸带字符。

  4. 模拟接受

     A	B
     $XqY$	$q$
     $Xq$	$q$
     $qY$	$q$

  5. 收尾

     A	B
     $q\#\#$	$\#$

Skolem问题

• 问题定义：一个定常线性递推数列中是否包含0
• 这个问题是/否可判定尚无定论。目前最好的结果是7阶（用前七个数递推后一个数）以下都是不可判定的（https://dl.acm.org/doi/fullHtml/10.1145/3531130.3533328）。注意：这意味着即使是简单的数列也可以蕴含图灵机的结构。

附：写出三个（维数较高的）整数方矩阵A、B、C，问能否令ABC=0也是不可判定的。不过我忘记这个问题的名称了（