计算理论6

结合几个例子介绍最通用的图灵机模型

定义

一条两端无穷长纸带 + 一个控制单元
- 这个控制单元可以是DFA或NFA，则定义出来的图灵机为DTM（Deterministic Turing Machine）或NTM（non-Deterministic Turing Machine），可以“读写”纸带的各个格子
- 以下主要讨论DTM
- 其实也有讨论多纸带的图灵机。以下讨论的图灵机只有一条纸带
形式化定义： $M = (Q,\Sigma,\delta,q_0,F,\Gamma,B)$
- 前面五个要素就是“控制单元”DFA的五大要素（所以其实写成 $M=(A,\Gamma,B)$ 也行）
- $\Gamma$ 是纸带上可以填写的字符，显然 $\Sigma \sub \Gamma$
- $B$ 指空白字符，纸带上默认的字符
- 停机：到达在 $F$ 中的特定接收/拒绝状态后就能停机。由于控制部分的DFA并非获取外部的有限输入，因此完全有可能永远不停机
- 状态转移定义和控制单元是DTM还是NTM有关：
  - DTM： $\delta:Q\times \Gamma \rightarrow Q\times \Gamma\times \{\leftarrow,\rightarrow \}$
  - NTM： $\delta:Q\times \Gamma \rightarrow 2^{Q\times \Gamma\times \{\leftarrow,\rightarrow \}}$
- 即状态转移根据当前状态和当前纸带上的字符确定下一步状态、当前指向的字符改写成何种字符、指针向左还是向右
- configuration（ID）：把纸带上的有效字符（非空白字符）段切出来，然后把当前状态写在当前指向字符的左边，这样形成的串可以表示图灵机某时刻的整体“状态”
  - 初始ID：设输入为 $x_1x_2...x_n$ ，则ID为 $q_0x_1x_2…x_n$ ，即指针初始位置一般默认指向输入串的第一个字符
  - 变化示例：当前指向 $x_1$ ，将格中内容改为 $y_1$ ，DFA状态转移到 $q_1$ 并向右移一格，则ID为 $y_1q_1x_2…x_n$
  - 可以记为 $q_0x_1x_2…x_n→y_1q_1x_2…x_n$ ，类似CFG中的“推导”
  - 同理可以定义出多步转移 $\rightarrow ^*$
- 接收条件：存在串 $\alpha,\beta$ （任意的就行），使得 $q_0w\rightarrow ^* \alpha q_F\beta,q_F\in F$ ，即让控制单元DFA能走到终止状态就行。

两个示例

示例1

$L=\{0^n1^n2^n|n\ge 1\}$ ，此前已证其非CFL
考虑令 $\Sigma=\{0,1,2\},\Gamma=\{0,1,2,X,Y,Z\}$
初始ID就遵照默认设置
方法：循环遍历纸带上的有效部分（输入的串部分），每次各改一个0，1，2为X，Y，Z，反复执行
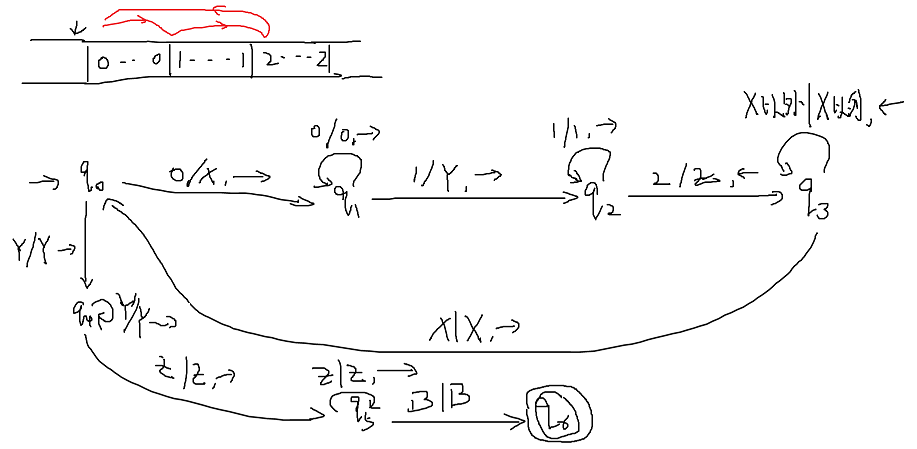
原则上可以加拒绝终止状态，但一般会像上图一样省略（无路可走就是拒绝接受）
如果希望保持到达终止态时输入串不变，也可以在 $q_6$ $q_{6}$ 后面再加一些状态负责恢复输入原状并把指针复位，这样就可以做成子程序方便调用
- 例如：考虑 $L=\{0^{n^2}1^{n^2}2^{n^2}|n\ge 1\}$ ，就可以先用一个TM负责判定012数量是否相同，再用一个TM负责判定是否平方数，然后把两个TM的控制部分合并起来
和计算机的重要区别：非随机访问。以上算法大致是 $O(n^2)$ 复杂度

示例2

$\{w\#w\|w \in \{ 0,1 \}^*\}$ ，其中#是一个分割字符，w是任意串。用pumping lemma同样易证非上下文无关
DTM构造思路：向右扫描，根据第一个 $w$ 中尚未被替换的第一个字符是0还是1进入不同的分支，若是0则作替换 $0\rightarrow X$ 然后向右找 $\#$ ，然后找第二个 $w$ 中的首个未被替换字符是否为0，若是则向左返回第一个 $w$ 中尚未被替换的第一个字符。若是1则同理。

优化与复杂度问题

事实上，示例1有更好的实现使得复杂度为O(nlogn)，但示例2必然是平方复杂度

示例1的更好实现

方便起见，用 $\{0^n1^n\}$ 来解释方法，这种办法可以拓展到示例1的情况
记前段0个数和后段1个数分别为 $n,m$
首先比较 $n$ 和 $m$ 的奇偶性是否相同，即比二者的个位
然后考虑比十位：方法是在扫描过程中每隔两个字符才做一次 $0\rightarrow X,1\rightarrow Y$ 的替换，且0段和1段的第一个字符总是替换，于是每轮替换后0或1的个数会分别变为 $floor(n/2),floor(m/2)$
同时，每趟扫描还能确定剩余的0或1的奇偶性，即相当于确定了十位、百位、……各个数位上是0还是1，于是逐位比较即可
于是整体复杂度为 $O(nlogn)$

示例1的另一种更好实现

是20年前某位本科学长提出的哦
考虑先设计子程序能够数出全0串的0的个数（把个数的二进制表示写到初始指针位置前面的纸带上）
方便起见，假设起始位置的左边一格有个#号作为分隔符（即使没有，也很容易加几个状态主动把#添上）
每次向右做一次 $0\rightarrow X$ 的替代，然后一直向左直到读入#后继续向左，把个数加一（注意进位），以下就是计数的子程序
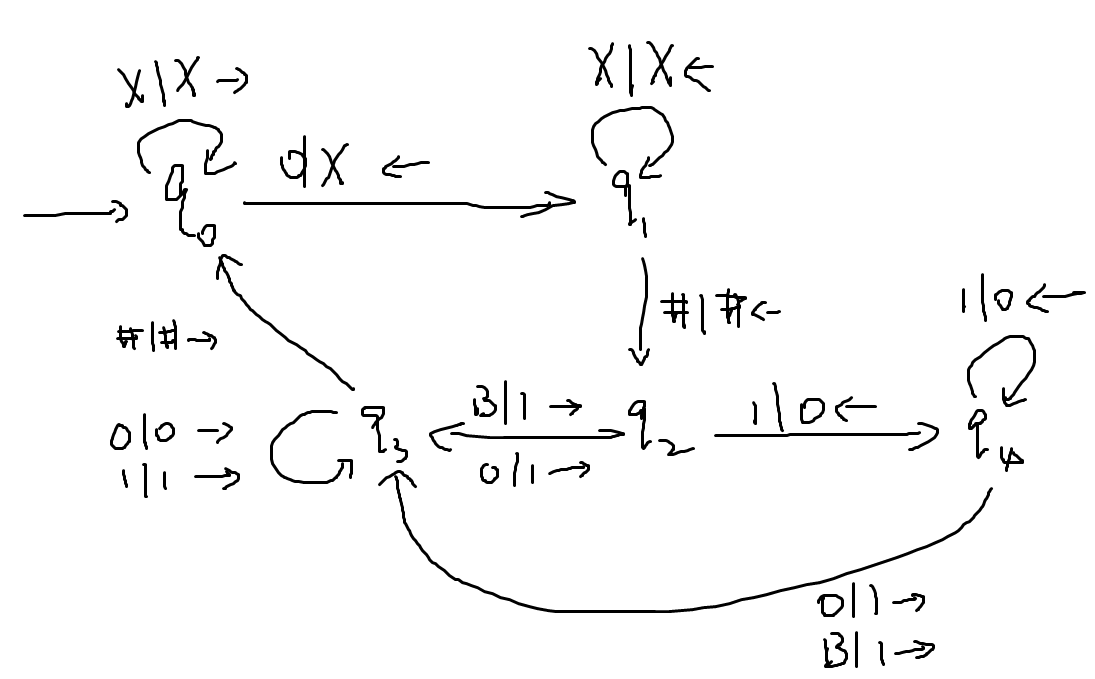
但这样显然仅仅计数部分耗时就是 $O(n^2)$
修改为拖拉机方法：每次向右做一次 $0\rightarrow X$ 的替代，就把#以及此前的计数结果向右平移一格。由于计数结果长度不超过 $O(logn)$ ，则这样计数部分复杂度就是 $O(nlogn)$
后面的比较不会超过 $(logn)^2$ 的复杂度（可以参考 $\{w\#w\}$ 案例中的比较方式），因此整体复杂度为 $O(nlogn)$

示例1的复杂度下限

示例1的复杂度下限就是 $O(nlogn)$

假设我们已经有一个能够完成示例1的DTM T，然后我们再在0段和1段的分界处“切”一刀，随后构造两个DTM A，B，分别负责交界线左侧和右侧的部分——也就是说，A和B共用T的控制部分，当T的指针在分界线左时A的指针就跟随T，否则就让B的指针跟随T。A和B可以通过观察被共用的T控制部分进行信息交流（即通过观察状态来通信）
- 每当T的指针穿过分界处时，控制权发生一次转移，就会发生一次这样的通信
可以假设A和B已经数好各自负责部分0或1的个数，然后进行通信获知二者是否相同
- 由于是证明下界，可以不管这里引入的时间复杂度，因此也不用管A、B具体是如何完成计数的——后面的通信环节就已经至少需要 $O(nlogn)$ 次操作了
引理（通信复杂度）若0和1的个数在 $O(n)$ 量级，则A、B至少需要进行 $O(logn)$ 次通信（或者说，通信量至少为 $O(logn)$ bit量级）才能判定A、B数出的个数是否相同。
- 直观证明：考虑整个通信历史，每bit的通信可以减少一半的未知性（减少一半的可能、引入一次分叉的机会），于是 $k$ bit通信只能引入 $2^k$ 种分支。
假设“切”一刀的位置不在0段和1段的分界线呢？
- 例如 $0000001111|111$
- 可以假设A在数完0（6个）后还能把分到自己这边的1个数也数出来（4个），然后作差(2个)，把2作为结果传给B。这样不会影响结果的正确性。和前面一样，我们不关心其复杂度和实现方式
- 当然，我们要求这样”切“的位置不能离01分界线”太远“，否则作差的结果是负数就不太好办了。只要差不是负数，这种方式总是可行的

复杂度下限证明

假设存在一个TM T能够以低于 $O(nlogn)$ 的复杂度完成示例1
则我们设输入串0和1的个数分别为 $n,m$ ，且方便起见不妨设 $2n>m>n$ （这样保证总长还是 $O(m+n)=O(n)$ 的）
针对我们给定的输入串，T的指针运动轨迹是确定的
于是考虑01分界线向左长为 $n/4$ 的段，这段中每个位置”切“开后，左右两部分计数都不会出现负数，因此总是可以像上文所述的方式构造TM A、B，而二者通信量为 $O(logn)$ ，则在每个位置上T指针都要左右来回穿越 $O(logn)$ 次。而这一段的长度为 $O(n/4)=O(n)$ ，于是光这一段的通信引入的时间复杂度就已达到 $O(nlogn)$ ，矛盾！

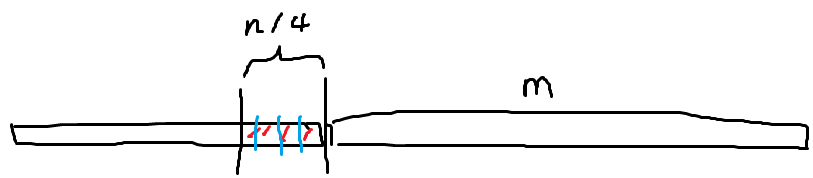
由于已经构造出 $O(nlogn)$ 的算法，因此这是下确界