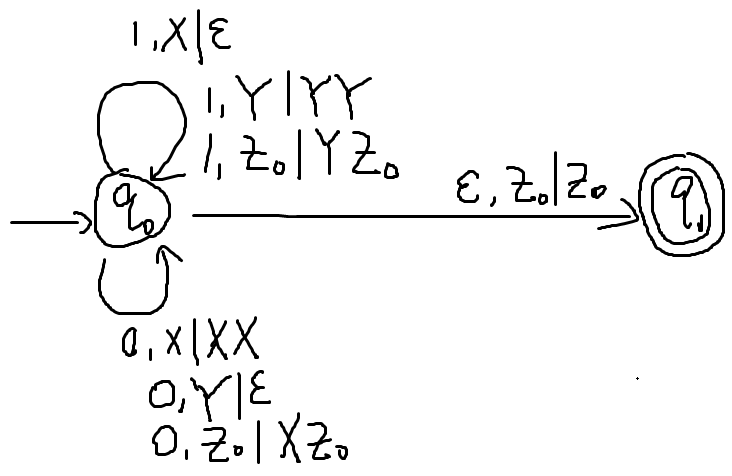计算理论5

简介下推自动机，其与上下文无关文法的关系，乔姆斯基范式，上下文无关文法的pumping lemma等内容。

下推自动机

Pushdown Automata，PDA。实际上用得不多。

定义

PDA $P=(Q,\Sigma,\delta,q_0,F,\Gamma,Z_0)$

• $\Gamma$表示一个栈（存储空间，和DFA/NFA区别的最重要的东西），$Z_0$表示栈底字符（这里定义的是接受态接收型PDA，则栈底字符不能动）
• 转移规则$\delta:Q\times \Sigma\times \Gamma\rightarrow 2^{Q\times \Gamma^*}$（也就是转移时要看一眼栈顶字符，且可以转移向多个状态（类似ε-NFA））
  • 注意：这里的ε-NFA不能改成NFA、DFA等，否则这样定义出的“PDA”计算能力会变弱，尽管ε-NFA，NFA和DFA计算能力是一样的
  • 每次转移都需要弹出栈顶字符，同时可以向栈里可以压入一个或多个字符；若压入ε则表示弹出栈顶字符（所以每次至多只能弹出一个栈顶字符！）

ID（instantaneous description，configuration）

• 一个ID的含义是$(q,w,\alpha)$，即PDA某个时刻的形态“切片”，或者说是$\delta$的自变量

  • $w$：剩下的字符
  • $α$：当前的栈的内容
  • $q$：当前状态

• 一个ID可以根据转移规则，运动到多个ID上。据此，$\hat\delta$也可定义出来

• 则PDA P接收的语言为$L(P)=\{w\in \Sigma | (q_0,w,Z_0)\rightarrow ^*(p,\epsilon,\alpha),p\in F\}$（所谓“接受态接收”，即能到接收态的串。箭头上的*代表多次转移）

  • 示例：$L=\{0^n1^n|n\ge 0\}$

  • 

    • $X$表示某个特定字符（无意义），栈中字符和串字符没有必然的联系
    • 注意：用pumping lemma易证这不是正则语言

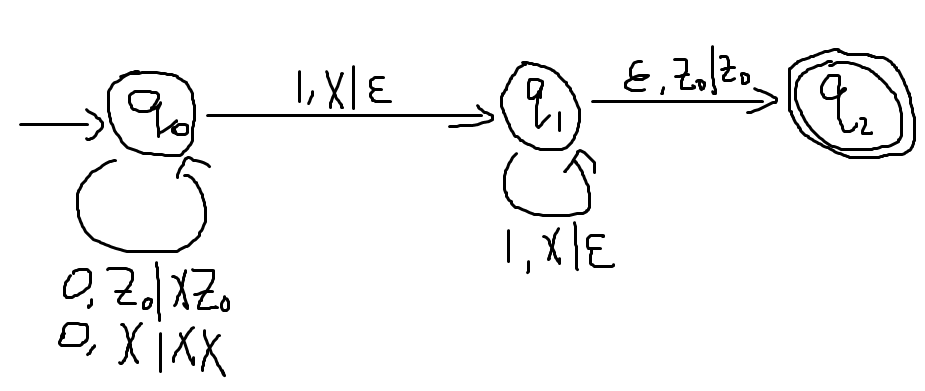
  • 示例：$0$和$1$的数量相同

    • 由于不能保证前缀中谁多，因此定义$Y$是$-1$，$X$是$1$，即可进行了

    

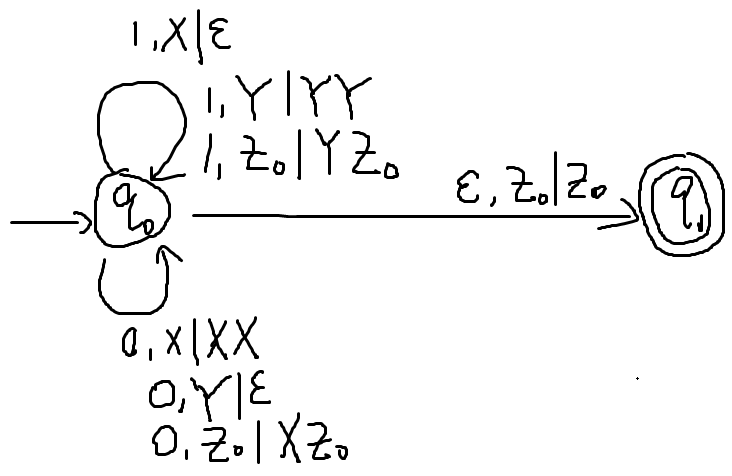
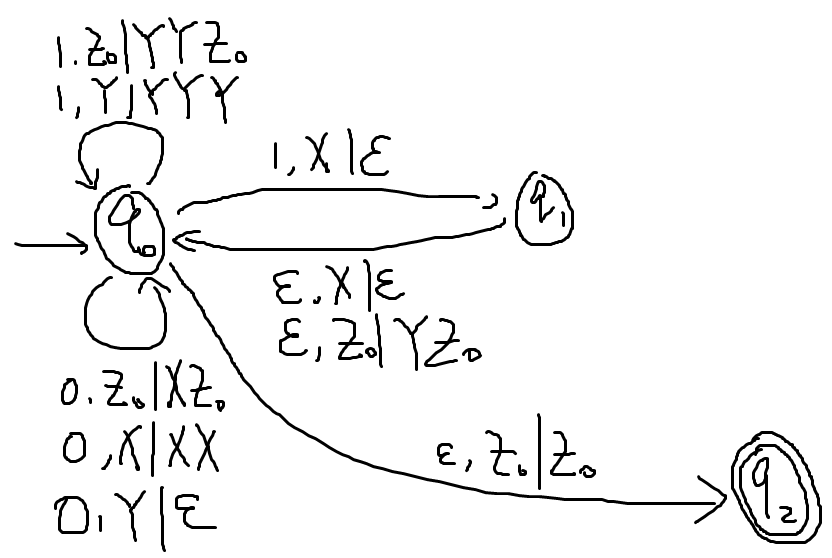
  • 示例：$L=\{w\in\{0,1\}^*|N_0(w)=2N_1(w)\}$，$N_x(w)$表示$w$中的$x$的数量

    • 则$0$表示“走$2$步”，$1$则回退$1$步，看能否回原点
    • 一次转移只能弹出一个字符，但也容易通过加状态实现弹出多个的效果
    • 用$X$和$Y$表示“正负”

    

    • 3倍4倍也类似了

等价性

定理 PDA和CFG能算的语言一样（即都能且只能计算上下文无关语言CFL）

• 任意CFG $G=(V,T,P,S)$，设法构造PDA $P$使得$L(G)=L(P)$

  • 举例：$S\rightarrow SS|0S1|1S0|ε$
  • 则先把$S$作为字符压入栈，然后模拟各个推导式（此时不接受字符）。于是在下图的$q_1$状态上可抵达的栈的各种可能将会包含所有在$L$中的串。
  • 接收字符则只接受终结字符，然后利用上一条继续在栈上推导
  • 最后若能让栈清空则表示和某个栈匹配，即输入的串在$L$中，故直接导向终结态

  

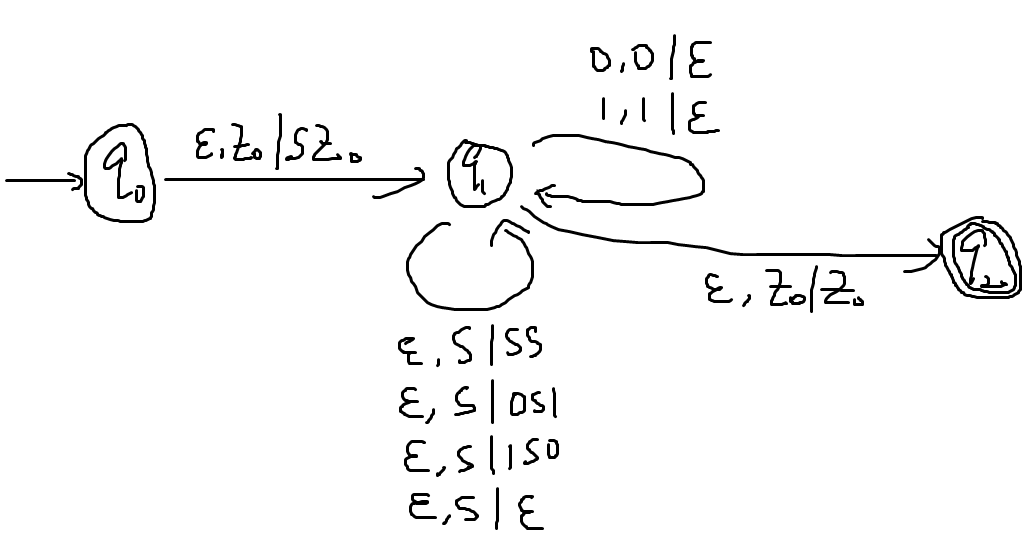
• 任意PDA $P$，设法构造CFG $G$使得$L(G)=L(P)$

  • 较为复杂，需要引入空栈接收PDA（和前面讨论的“接受态接收PDA”“区分），其定义为$L(P)=\{w\in \Sigma | (q_0,w,Z_0)\rightarrow ^*(r,\epsilon,\epsilon)\}$，即允许把$Z_0$弹出来（弹出后即接收），且在读完输入串后停留在$r$上时，不要求$r$是接受态
  • 然后说明任意接受态接收PDA都能改造成空栈接收PDA：只用在接受态接收PDA $P$的基础上考虑其终止状态，加个状态就成了空栈接收PDA $P’$
  • 
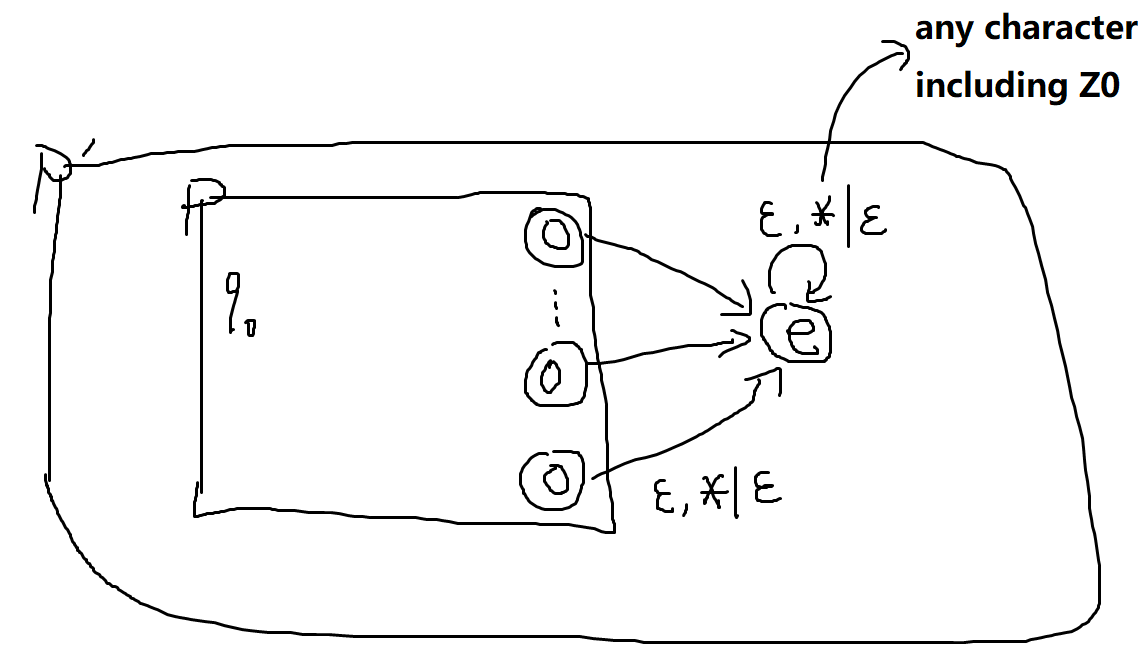
  • 因此只用构造$G$能表达空栈接收PDA $P'$
    • $G$的终结符集合$T$就是$Σ$，非终结符集合$V$为一个三元组的集合，即$[q,X,p]\in V$，其中$q,p$都是PDA的状态
    • 这个非终结符（变量）的含义是，若$[q,X,p]\rightarrow w$，$w$满足当从$q$状态读完串$w$后能转移$p$状态，与此同时只会把$X$字符弹出栈。
    • 下推方法为三部分：
      • $S\rightarrow [q_0,Z_0,p_0]|[q_0,Z_0,p_1]|...|q_0,Z_0,p_n]$，即以各种可能触发空栈（注意$q_0$是其实状态，$p_0\sim p_n$遍历了PDA的所有状态）
      • $\delta(q,a,X)\rightarrow (p,\epsilon)$对应下推规则$[q,X,p]\rightarrow a$（这里的$\epsilon$表示弹出$X$后不补入任何字符）
      • $\delta(q,a,X)\rightarrow (r,Y_1Y_2...Y_k)$对应下推规则$[q,X,p]\rightarrow a[r,Y_1,m_1][m_1,Y_2,m_2]...[m_{k-1},Y_k,p]|a...|a...|a...$（这里要列举所有从$r$到$p$的路径：$r\rightarrow m_1\rightarrow m_2\rightarrow ...\rightarrow p$）

CFG的乔姆斯基范式

Chomsky Normal Form

• 一般的CFG推导规则的箭头右端是没有限制的，乔姆斯基范式就是要规范这一点

• 期望只有两种推导模式：$A\rightarrow BC,A\rightarrow a$，$A$，$B$，$C$是某几个非终结符（变量），$a$是某个终结符，$B$、$C$可以等于$A$，且不允许有$A\rightarrow \epsilon$形式的推导

  • 于是推导次数就固定了：长为$n$的串至多经过$n-1$次$A\rightarrow BC$形式的推导和$n$次$A\rightarrow a$形式的推导即可确认是否在该CGL中。
  • 在规范化中，可能原语言中有ε而规范化后没有了：需要特殊处理
  • 规范化主要处理
    • 终结符和非终结符混合
    • 右端有多个$S$
  • 解决方法：添加字符
    • 例如：$S\rightarrow 0S1|0S0S$
    • 则$S\rightarrow XSY,X\rightarrow 0,Y\rightarrow 1$
    • $S\rightarrow T_1Y,T_1\rightarrow T_2S,T_2\rightarrow T_30,...$
    • 如果遇到$A\rightarrow B,B\rightarrow C,...$，则直接$A\rightarrow C$即可（其实是在看连通性）
    • 小心ε，例如$A\rightarrow \epsilon,B\rightarrow AC$，则改造后删去前一条后要加上$B\rightarrow AC|C$（之后还要根据$C$后推的结果把这个式子的$C$换掉）

• 好处：范式下解析树一定是二叉树（不一定满），示例

  

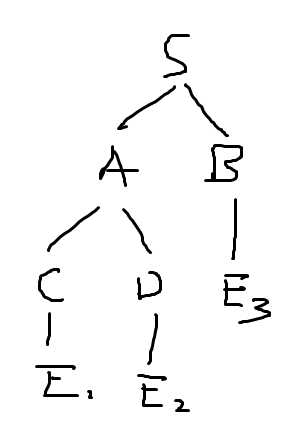
• 于是可以得到CFG的pumping lemma：若语言$L$是CFL，$G$是对应文法，则存在正整数$N$，使得$\forall z \in L,|z| > N$时，可以将$z$分解为五段$z=uvwxy$，且满足：

  • $|vwx|\le N$
  • $|vx|>0$
  • $uv^kwx^ky\in L,\forall k \ge 0$

• 证明：

  • 把$G$改写成乔姆斯基范式，则解析树是二叉树（除叶结点）

  • 若二叉树高为$h$，则叶子数最多为$2^h$（注意：乔姆斯基范式下所有叶节点都没有兄弟），于是能生成的串长不超过$2^h$

  • 于是令$N=2^{|V|+1}$（$V$是变量集），则$2^h > N = 2^{|V|+1}$，于是从根节点到最深叶结点（的父节点）的路径经过$h+1$个节点，超过变量数，因此这条路径上必然至少有两个节点用的是相同的变量

  • 于是可以把深度更浅的节点对应的子树剪切粘贴到深度更深的节点上（见下图，这是由于相同的变量总是可以使用相同的规则进行下推），就可以直接得到$uv^2wx^2y\in L$，如此类推即证。

  • 至于前两个结论直接计算即可

    

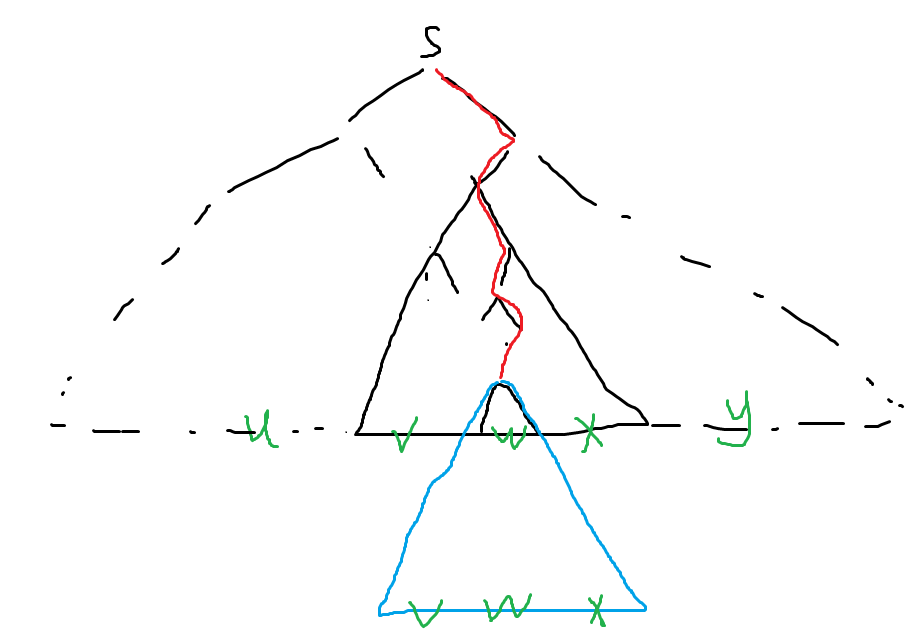
• 示例

  • $0^n1^n$：上下文无关可算。但$0^n1^n2^n$上下文无关不能算
  • 直观理解：单个栈的存储能力也有限制，不能同时判断三个值相等
  • 用pumping lemma反证，令$z=0^{N+1}1^{N+1}2^{N+1}=uvwxy$
    • $v$中没0：则$v$、$w$中只包含1和2，0不能被pump，导致数量不同。
    • $v$中有0：则由于$|vwx|\le N$，则$x$不包含2，故2不能被pump，导致数量不同。

• 又例

  • 类似$ww$形式的语言（前一半和后一半相同）不是上下文无关的
  • 证明：考虑$z=0^{N+1}1^{N+1}0^{N+1}1^{N+1}=uvwxy$
  • 很容易看出，无论$vwx$在哪都没法在pumping后让前后两半相同了

• 又例：回文串是上下文无关的（很容易写出其CFG）

• 注意：上下文无关在补集意义下不封闭，例如类似$ww$形式的语言虽然不是上下文无关的，但其补语言是上下文无关的！（后证）

• 又例

  • $\{0^{n^2}|n\ge 0\}$也不是上下文无关的（前面已经证明过不是正则的）
  • 证明：$z=0^{N^2}=uvwxy$，pump后得到$0^{N^2+(k-1)l},l=|v|+|x|<N$，但$N^2$以后的下一个完全平方数是$N^2+2N+1$，取$k=2$之类就显然不是完全平方数了
  • 这种单字符语言的证明和正则语言的pumping lemma过程一样
  • 进一步地可以得到论断：单字符语言是正则的当且仅当它是上下文无关的（即单字符情况下上下文无关没法比正则算更多的东西）（证略）

CFL性质

• 哪些运算对上下文无关封闭？

  如何证明一个语言是上下文无关的？

  • 导出其文法
  • 构造其PDA

  • $L_1\cup L_2,L_1L_2,L^*,f:\Sigma_1\rightarrow \Sigma_2^*,f^{-1}$保持（逆映射定义参见正则语言部分）。这些可以通过直接构造文法证明。
  • $L_1\cap L_2$不保持
    • 例子：$L_1=\{0^*1^n2^n\},L_2=\{0^n1^n2^*\}$，这两个的上下文无关性可以通过其连接不变性证明（如$\{0^*\},\{1^n2^n\}$分别都是上下文无关的，因此其连接也是）；而并则为$\{0^n1^n2^n\}$，前面已证这并非上下文无关
    • 原因：在证明正则语言交的不变性时，新构造的DFA每个状态都是一个状态对，因此可以并行地同时模拟两个DFA的运行；但2个PDA就有两个栈没法二合一。
    • 如果有两个栈，则PDA计算能力和图灵机相同。
    • 如果能让合并后栈只有一个，则并能保持封闭。如一个上下文无关语言和一个正则语言的并是上下文无关的。
  • $\bar{L_1}$不保持
    • 例子：前面的：并非$ww$形式的串组成的语言$L$是CFL
    • 证明：$L$=”奇数长串“并上”偶数长且前半后半不同的串“
    • 奇数长的串是正则的：$S\rightarrow 0S0|1S1|0S1|1S0|0|1$
    • 偶数长的串则有奇妙的镜像性质：假定总长为$2n$，且$i,i+n$两个位置上的字符不同，则将串拆成长为$2(i-1),2n-2(i-1)$的两段后，$i,i+n$两个位置恰好是两段的中点。
    • 
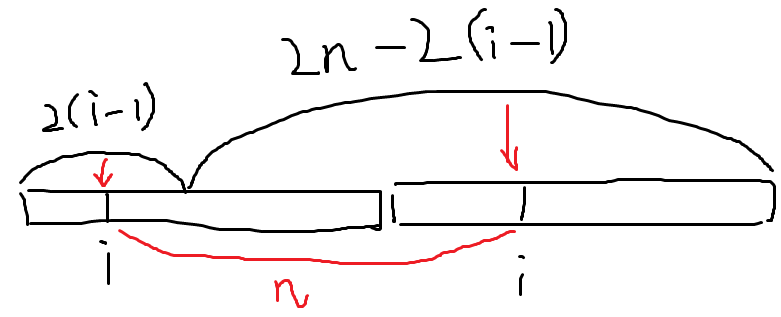
    • 于是这种串总是可以拆成两个中心字符不同的奇数长的串。即可由此得到CFG：
      • $A1$表示以0为中心的奇数长串，$A_1\rightarrow 0A_10|0A_11|1A_10|1A_11|0$
      • $A2$表示以1为中心的奇数长串，$A_2\rightarrow 0A_20|0A_21|1A_20|1A_21|1$
      • $S\rightarrow A_1A_2|A_2A_1$

• 以下问题图灵机均不可判定（不可计算）：

  • 判断两个CFL是否相同？
  • 判断某个CFL是否能表达所有串？
  • 判断两个CFL的交是否为空？
  • 判断某个CFG是否歧义？判断某个CFL是否固有歧义？

• 以下问题有多项式时间算法：

  • 判断某个串x是否在CFG表示的语言中
    • 先把CFG改造成乔姆斯基范式
    • 然后DP求解，三维表，三个轴分别为变量、$i$、$j$，每个格子的内容是对应的变量能否生成出$x_ix_{i+1}...x_{j}$
    • 初始条件只能填写$i=j$的格子，然后考虑$j=i+1,j=i+2,...$（即由长度由小到大递推）
    • 填$(A,i,j)$：看$A$在乔姆斯基范式中所有$A\rightarrow BC$形式的映射，则填入的值是所有$\cup_{i\le k<j}(B,i,k)\cap(C,k+1,j)$的并（按：用交并表示了与或）