第三视点

所见的所有东西

0%

计算理论4

发表于 分类于

简介上下文无关文法和上下文无关语言。

CFG，Context Free Grammar

  • 即上下文无关文法
  • 反义：Context Sensitive，即上下文有关

非形式化定义的例子——回文串

  • 考虑Σ={0,1}\Sigma = \{0,1\}的回文语言LpalL_{pal}
  • 容易验证这不是正则语言：考虑0n10n0^n10^n形式的串，即可类前用pumping lemma证明这不能是一个正则语言。
  • 可以考虑一种递归式的定义：
    • 空串ε，0，1是回文串
    • w∈Lpal→0w0,1w1∈Lpalw\in L_{pal}\rightarrow 0w0,1w1 \in L_{pal}

CFG就是针对这种递归式文法的一种形式化定义。

CFG正式定义

  • 用GG标识，G=(V,T,P,S)G=(V,T,P,S)
    • VV：非终结符（或称变量）的集合，是有限集。每个变量都是具有一定特征的串的集合（即其实每个变量也都是一个语言）。
    • TT：终结符的集合，是有限集。其实就是目标语言的字符集。
    • P:V→(V∪T)∗P:V\rightarrow (V\cup T)^*：推导规则（可以有很多条左边这种推导规则，但规则总数是有限的）。每条推导规则的形式都是由一个变量（head）到变量和终结符混合的一个串（body）。
    • SS：起始符（是一个变量），是VV的元素。

回文串的形式化定义：

  • 非终结符集{P}\{P\}，终结符0,10,1，起始符PP
  • 推导规则：
    • P→ϵ,P→0,P→1P\rightarrow \epsilon,P\rightarrow 0, P\rightarrow 1
    • P→0P0,P→1P1P\rightarrow 0P0,P\rightarrow 1P1
  • 实例化的推导过程可以用⇒\Rightarrow符号，如P⇒0P0⇒01P10⇒0110P\Rightarrow 0P0\Rightarrow 01P10\Rightarrow 0110。此时可以用⇒∗\Rightarrow^*表示多步推导。

一些表达习惯：

  • 小写字母、数字等是终结符
  • 大写字母是变量
  • w,zw,z有时表示仅有终结符构成的串，即最终语言中的一个元素
  • X,Y,ZX,Y,Z有时也是终结符
  • 希腊字母表示终结符和变量混合构成的串（即推导的中间结果）

左推、右推

  • Leftmost/Rightmost Derivations，即每次推导总是只对当前串最左/最右的变量使用推导规则，可以记为⇒lm,⇒rm\Rightarrow_{lm},\Rightarrow_{rm}。也可以加*表示多步推导。
  • 定理 A⇒∗w,A⇒lm∗w,A⇒rm∗wA\Rightarrow^* w,A\Rightarrow^*_{lm}w,A\Rightarrow^*_{rm}w三者相互等价，即每个推导都有与之等价的左推和右推。

CFL，Context Free Language

  • 即上下文无关语言。若GG是CFG，则L(G)={w∈T∗∣S⇒∗w}L(G)=\{w\in T^*|S\Rightarrow^* w\}就是CFL。
  • 句式（Sentential Forms）：能被起始符SS推导出来的串（可以包含变量）就是一个句式。
    • 句式的集合就是{α∈(V∪T)∗∣S⇒∗α}\{\alpha \in (V\cup T)^* | S\Rightarrow^* \alpha\}。显然，CFL是该集合的子集
    • 若某串能被起始符连续左推/右推出来，则称为左推句式/右推句式

解析树，Parse Trees

  • 即表示推导过程的树，其构成为：
    • 非叶节点是变量
    • 叶结点是变量或终结符或空串。但当叶结点是空串时，它必须是其父节点的唯一子节点（即没有兄弟）
    • 若某非叶节点为AA，其子节点为X1,X2,...,XkX_1,X_2,...,X_k，则A→X1X2...XkA\rightarrow X_1X_2...X_k是推导规则中的一条（可见如果允许空串有兄弟节点，则可以加任意多个空串兄弟，树的结构就乱了）。
  • 解析树的结果（yield）：根节点为起始符时，叶节点（此时要求所有节点完全展开，即此时叶结点只能是终结符或空串）按照遍历中的顺序构成的串（只包含终结符）
  • 定理 A⇒∗w,A⇒lm∗w,A⇒rm∗wA\Rightarrow^* w,A\Rightarrow^*_{lm}w,A\Rightarrow^*_{rm}w以及“存在以AA为根、结果为ww的解析树”这四条论断等价。
    • 证明可使用递归。其中值得注意的是由A⇒∗wA\Rightarrow^* w导出A⇒lm∗wA\Rightarrow^*_{lm}w：
    • 根据树的高度做递归。设高度为nn时原命题成立，则高度为n+1n+1时如下图：
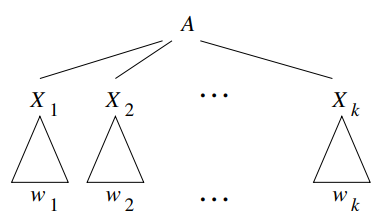
    • image-20230416164843156
    • 则当XiX_i是变量时，即可将以其为根的子树（该子树高度不会超过nn）改为左推的形式。
    • 这里再嵌套一层递归：
      • 由于AA本身也是一个串，且其最左的变量就是AA，因此A⇒lmX1X2...XkA\Rightarrow_{lm}X_1X_2...X_k成立。
      • 由于我们已经改造过各个XiX_i下的子树，于是可知A⇒lm∗w1X2...XkA\Rightarrow_{lm}^*w_1X_2...X_k成立，而w1X2...Xk⇒lm∗w1w2...Xkw_1X_2...X_k\Rightarrow_{lm}^*w_1w_2...X_k成立，由⇒lm∗\Rightarrow_{lm}^*的传递性（易证），则知A⇒lm∗w1w2...XkA\Rightarrow_{lm}^*w_1w_2...X_k，……，最后即得A⇒lm∗w1...wkA\Rightarrow_{lm}^*w_1...w_k，得证。
    • 右推也类似。

歧义性

示例：四则运算

  • 四则运算文法，+，*（简便起见只用3、4、5三个数）
    • G:S→S+S∣S∗S∣3∣4∣5G:S\rightarrow S+S|S*S|3|4|5（注意推导规则可以合在一起写）
    • 考虑5+3∗45+3*4的文法树
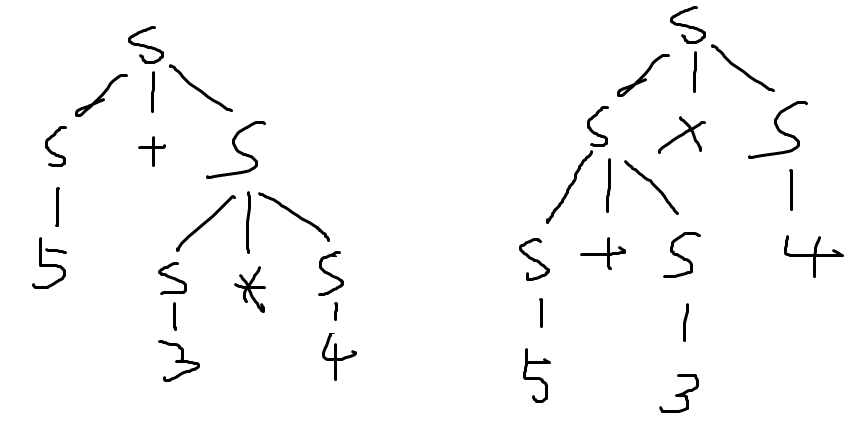
    • image-20230329203700973
    • 有两棵不同的语法树，因此这个式子是有歧义的（这就是歧义的定义。某个CFL只要有一个能产生它的CFG有歧义，则此CFL也有歧义。）
    • 去除歧义性的方法：改造语法（当然，有的文法是不可能去除歧义性（称为“固有歧义”））（改造：指不会改变其能计算的语言）
    • 本质上就是设置优先级，于是要求T必须是一个连乘积项(3*4*5之类)，例如：
    • S→S+T∣T,T→T∗T∣3∣4∣5S\rightarrow S+T|T, T\rightarrow T*T|3|4|5
  • 固有歧义（Inherent Ambiguity）：任何表达这种语言的CFG GG都是有歧义的
    • 示例：L1={0n1n2m3m∣m,n≥0},L2={0n1m2m3n∣m,n≥0}L_1 = \{0^n1^n2^m3^m|m,n\ge 0\},L_2 = \{0^n1^m2^m3^n|m,n\ge 0\}，考虑L1∪L2L_1\cup L_2，则这种语言中形如0k1k2k3k0^k1^k2^k3^k的串总是有两种生成方法
    • （显然，语言的并是不改变上下文无关性的）
    • 注意：歧义性和固有歧义性是不可判定的（图灵机不可算）

需要注意的是：必须是解析树不同才是歧义！有时推导看上去不同，但其实解析树是一样的。例如以下情况不是歧义：

E⇒E+E⇒I+E⇒a+E⇒a+I⇒a+bE⇒E+E⇒E+I⇒I+I⇒I+b⇒a+b\begin{aligned} & E \Rightarrow E+E \Rightarrow I+E \Rightarrow a+E \Rightarrow a+I \Rightarrow a+b \\ & E \Rightarrow E+E \Rightarrow E+I \Rightarrow I+I \Rightarrow I+b \Rightarrow a+b\end{aligned}

但如果限定为左推/右推则可得到有意义的结论：若某个串可以通过不同的左推/右推得到，则其有歧义。（证略，注意上面给的示例一个是左推一个是右推。）

欢迎关注我的其它发布渠道