计算理论2

简要介绍正则表达式。

正则语言（Regular language）、正则表达式（Regular expression）

定义

• 正则表达式的递归式定义

1. 最简单的正则表达式（递归基）

   • 空集$\empty$，对应的正则语言就是空集$\empty$
   • 空串$\epsilon$，对应的正则语言就是$\{\epsilon\}$
   • 任意单字符$a$，对应的正则语言是$\{a\}$

2. 进一步定义其他正则表达式（$L(E)$表示正则表达式$E$对应的正则语言）

   • 或：$L(E_1+E_2)=L(E_1)\cup L(E_2)$

   • 连接：$L(E_1E_2)=L(E_1)L(E_2)=\{w_1w_2|w_1\in L(E_1),w_2\in L(E_2)\}$

   • （克林）闭包：$L(E^*)=(L(E))^*$

• 能用正则表达式表示的语言就是正则语言（$\{L(E)|E\space is\space a \space regular\space expression\}$）

示例

• 例：由$0\sim9$构成的四位数的正则表达式：$(0+1+2+3+...+9)^{4}$
• 例：$L=\{w\in \{0,1\}^*|\#0\space in\space w\space is\space even\}$：
  • $1^*$表示若干个（0个~任意个）1
  • 于是对应的正则表达式可以写成$1^* (0 1^* 0 1^*)^*$
  • 即把符合条件的串剪成两个0两个0的段，当然要小心没有0的串！
• 例：$L=\{w\in \{0,1\}^*|1010\space is \space substr\space of \space w\}$，对应的正则表达式$(0+1)^*1010(0+1)^*$
• 例：$L=\{w\in \{0,1\}^*|\#0,\#1\space in\space w\space are\space both\space even\}$：
  • 首先00和11这两种正则表达式可以随便放，即$(00+11)^*$
  • 总长必然是偶数，因此可以两位两位地看
  • 显然01，10这两种子串出现的总次数也是偶数；11、00这两种子串则可任意多
  • 于是把00+11当成1，10+01当成0，即转化为上面已解决的问题
  • 即$(00+11)^*((01+10)(00+11)^*(01+10)(00+11)^*)^*$
  • 当然，正则表达式未必唯一
• 正则表达式和NFA类似，没法在多项式时间内最小化。但DFA的最小化是可以在多项式时间内完成的（这部分内容见后）。

等价性

定理 DFA、NFA和正则表达式能表达的语言都一样（即都能且只能表达正则语言）。

• 证明：DFA和NFA的等价性已证。则以DFA为例，

• 首先考虑为某个DFA找出对应的的正则表达式

• 例：

  

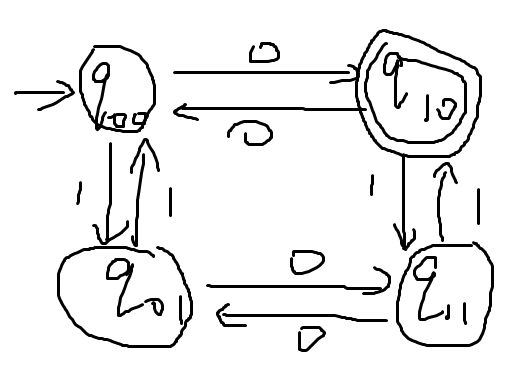
• 然后添加带正则表达式的边逐步替代普通的边，需要逐个状态地消去，例如下图中就需要添加带正则表达式的边以取代q01状态的功能

• 

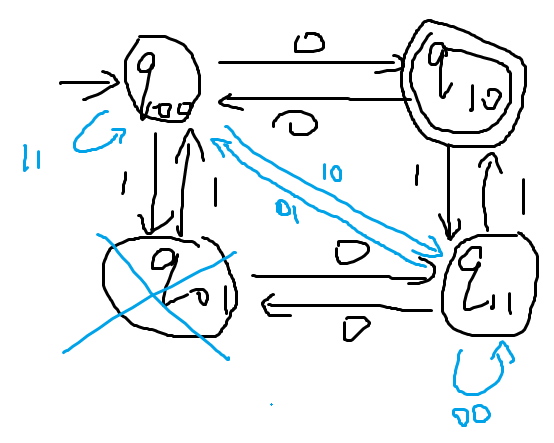
• 在添加四条带正则表达式的边后，q01这个状态所有输入输出都表达过了，所以可以消去了

• 

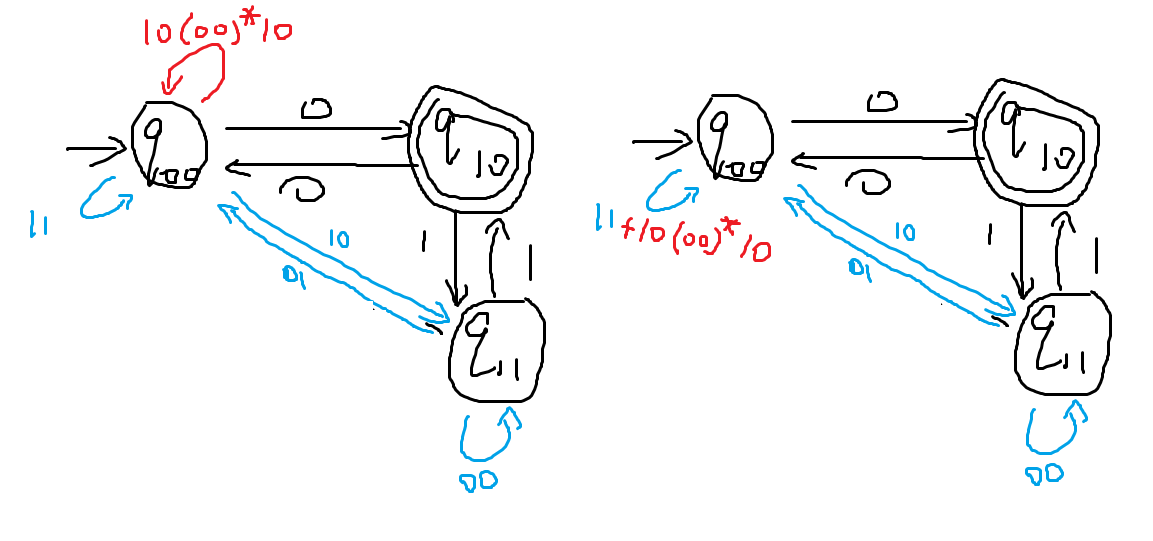
• 同理，接下来需要添加边来取代q11的功能（即只看经过q11的路径），这里需要注意自环要使用*运算，且同始同终的边的正则表达式可以+或起来变成一条边（上图没有完全化简完，仅作示意）

• 最后通常会变成这样一个形式

  

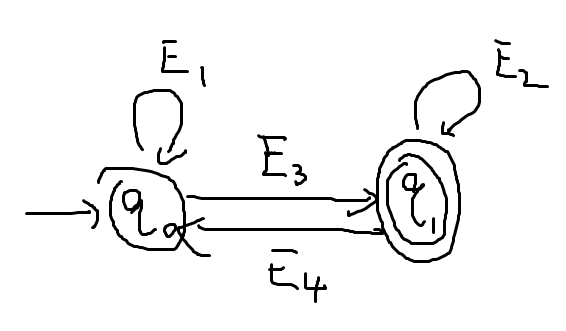
• 于是可以写成$E_1^*E_3(E_2+E_4E_1^*E_3)^*$

这部分的严格构造方式：

设DFA $A$ 有n个状态$\{1,2,...,n\}$，记$R^{(k)}_{ij}$为所有能从$i$状态到$j$状态，且中途不会经过编号大于$k$的状态的串（$i$或$j=k$是允许的）所对应的正则表达式。随后动态规划填表即可。

递归式为$R_{ij}^{(k)}=R_{ij}^{(k-1)}+R_{ik}^{(k-1)}(R_{kk}^{(k-1)})^*R_{kj}^{(k-1)}$

注：这个方法显然是多项式复杂度。

• 其次考虑为某个正则表达式构造对应的NFA

  • 正则表达式本身是递归构造。为递归基构建NFA很容易。
  • 然后关注递归规则，当$E_1$、$E_2$两个正则表达式都有对应的NFA时：
  • $E_1+E_2$：注意不能简单地像下图一样并起来
    • 
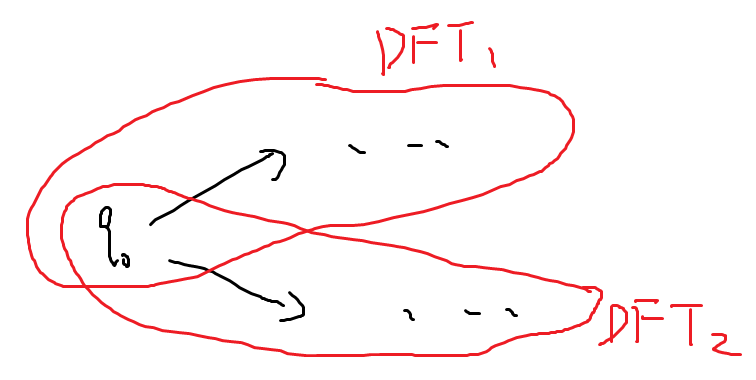
    • 例如接受偶数个0和接受3的倍数个0的正则语言是$(00)^*+(000)^*$
    • 则下图NFA可能接受“00000”，不满足原意
    • 
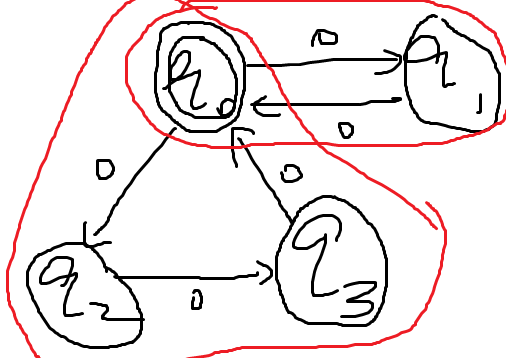
    • 于是需要ε-NFA：允许箭头上出现ε，即不读任何东西也能转移，这样就不会退回来导致上面的问题了
      
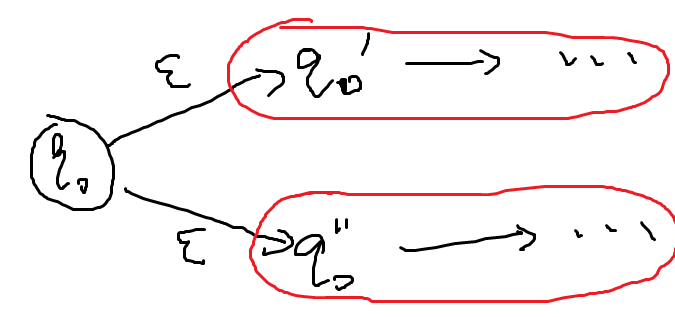
    • 现在需要证明ε-NFA和DFA等价，这只需要用和上次课相同的子集构造法即可证明
  • 用ε-NFA还可以证明$E_1E_2$和$E^*$也可以构造对应的ε-NFA，如下所示：
  • 
  • 

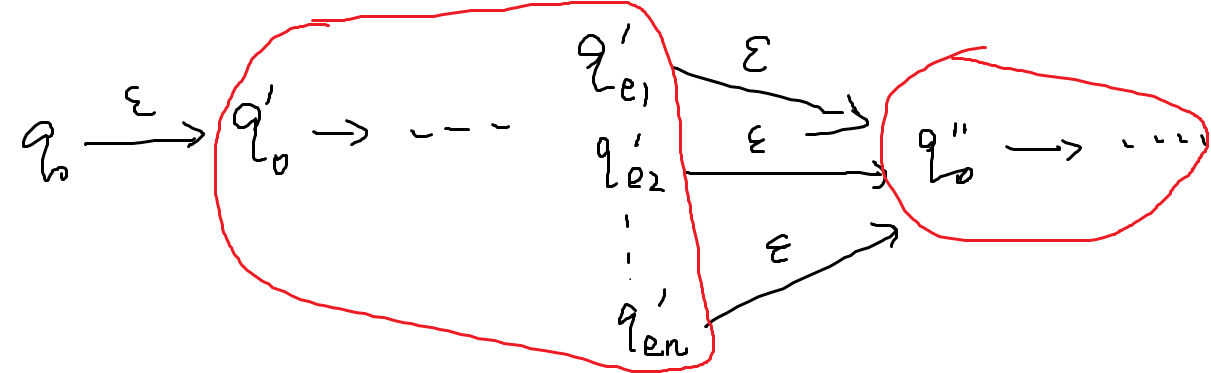
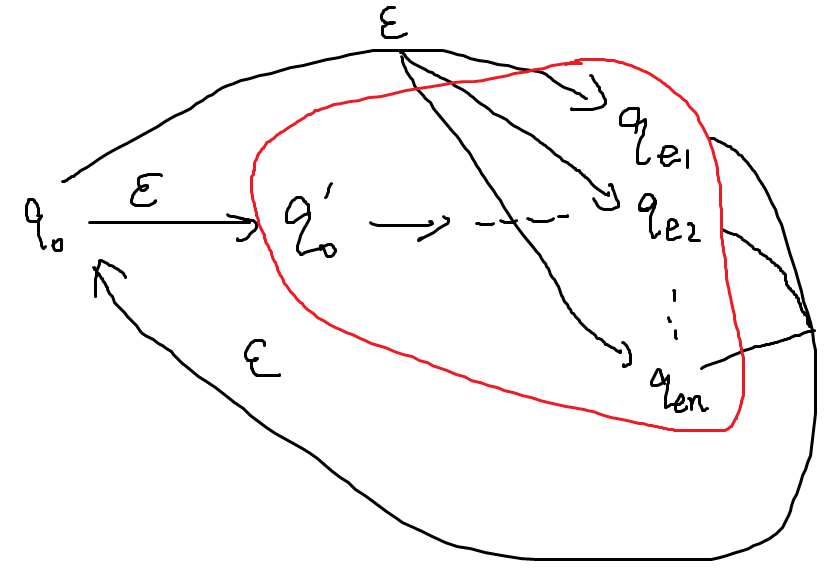
不能计算的东西

定理 存在DFA不能计算的语言

• 注意DFA实际上没有记忆，或者说由于状态有限，因此塞进去太多东西会导致状态重复出错。寻找不可计算的语言就需要由此作为突破口。
• 性质：正则语言的Pumping Lemma
• 设$L$是正则语言，则必然存在一个和$L$有关的自然数$M$，使得$L$中任意的$w$若满足$|w|>M$，则$w$一定可以分解成$w=xyz$的形式，且
  1. $|xy|<=M$
  2. $|y|>0$
  3. $xy^kz\in L,\forall k\ge 0$，如$xz,xyz,xyyz,xyyyz,…$
• 证明：$L$正则，则存在DFA $A$使得$L=L(A)$
• 这个DFA只有有限个状态，则取$M=|Q|+1$（取得比$|Q|$大就行，$Q$是状态集）
• 当$|w|>M$时，设$w=w_1w_2...w_t,t>M$，则$\hat{\delta}(q_0,w_1),\hat{\delta}(q_0,w_1w_2),...,\hat{\delta}(q_0,w_1...w_t)$都在$Q$中，由抽屉原理可知其中必然有重复的状态，这个多次出现的重复状态必然代表了一个有向回路，则将这个回路取作$y$，此前为$x$，此后为$z$即可。
• 利用Pumpling lemma即可提出反例：$\{L=0^*1^*|\#0=\#1\}$不是正则表达式
  • 反证，假设是正则表达式，则存在M，考虑$w=0^M1^M\in L$，则$w=xyz,|xy|\le M$，则$x$和$y$都是一段0，而y可以任意复制增减，于是矛盾。
  • 后面有的计算模型可以计算这个语言。
• 考虑把上面的语言取个“反”，即0和1的数量不一样多（注意不是关于$\{0,1\}^*$取了补集，因为可以有1开头的串！），则这个语言也不是正则的！
  • 反证：考虑$0^M1^{M!+M}\in L$，则还是分割成$xyz$，$x$、$y$都是0组成的串，且$y$的长度不会超过$M$，于是$k=M!/y$的长度就是一个整数，则$xy^{k+1}z$的前半段多出了$y^k=M!$个0，于是插在原本的$M$个0中就有了$M!+M$个0，和1的数量相同，导出矛盾
• 其他不能计算的语言：$\{0^{n^2}|n\in N^*\}$,$\{0^p|p\space is \space prime\}$,$\{0^p|p\space isn't \space prime\}$
  • 第二个例子的证明：正则则存在M，任取素数p>M（隐含地使用结论：素数有无穷多个），则$0^p=xyz,y=0^l,l\le M$，$xy^kz=0^{p+(k-1)l}$，取$k=p+1$，则长度为合数，故矛盾
  • 第三个证明：可以直接用补集转换为对第二个例子的讨论。
  • 直接证明则假设正则，则$0^n=xyz,y=0^l,xy^kz=0^{n+(k-1)l}$，然后考虑如何取k使得长度变成素数。
  • 迪利克雷定理：任意等差数列，只要首项和公差互质，则该数列中有无穷个素数（不互质则显然该数列中没有素数）（该定理的证明需要解析数论）。
    • 特例：首项和公差取为1，则可以证明素数有无穷多个；首项取成1，再把公差去成2，3，……则可知有无穷多个素数除2或3或……余1。（不过这个结论和本题无关）
  • 于是由于$l$不超过$M$，则取$p>M,n=p^2$，则$p^2$本身是合数，且必然和$l$互素，用迪利克雷定理即知随着$k$增加会有无穷多个素数出现，矛盾。
  • 其实也有办法可以绕过迪利克雷定理（待补充……

更多性质

• $L$正则，则$\bar{L}$也正则（证明和之前DFA一样。注意NFA的此项性质不能直接用补集法证明，需要子集展开后再补集才行）
• 除补集操作外，并交对正则也是封闭的（证明的时候只用把并证明即可）
  • 若想直接证明交，则考虑令$Q=Q_1\times Q_2$，……
• 连接、*操作也是封闭的
• 设字母表$\Sigma_1,\Sigma_2$，存在$f:\Sigma_1\rightarrow \Sigma_2$，设第一个字符表上存在正则语言$L$，则$f(L)=\{f(x)|x\in L\}$也是正则的。
• 设字母表$\Sigma_1,\Sigma_2$，存在$f:\Sigma_1\rightarrow \Sigma_2^*$，设第一个字符表上存在正则语言$L$，则$f(L)$还是正则的。原理：正则语言有一个正则表达式，把正则表达式的符号换成$\Sigma_2^*$对应的串即可得到$f(L)$的正则表达式。既然有正则表达式那这个语言显然就是正则的。
• 设字母表$\Sigma_1,\Sigma_2$，存在$f:\Sigma_1\rightarrow \Sigma_2^*$，设第二个字符表上存在正则语言$L$，定义逆映射$f^{-1}=\{w\in\Sigma_1^* | f(w)\in L\}$，则$f^{-1}(L)$还是正则的
  • 例：$f:\{a,b\}\rightarrow \{0,1\}^*,f(a)=0,f(b)=00$，则$f^{-1}(000)=\{aaa,ab,ba\}$
  • 证明：借助DFA，针对$L$有一个DFA（记为$A$）
  • 然后新自动机的构造方法就是针对$A$的每个状态，把$a$和$b$的像输入$A$，看输出能跑到哪里，则新自动机的转移终点就到对应的$A$中的状态，如此逐步地把$f^{-1}(L)$对应的DFA构建出来
  • 例：
  • 
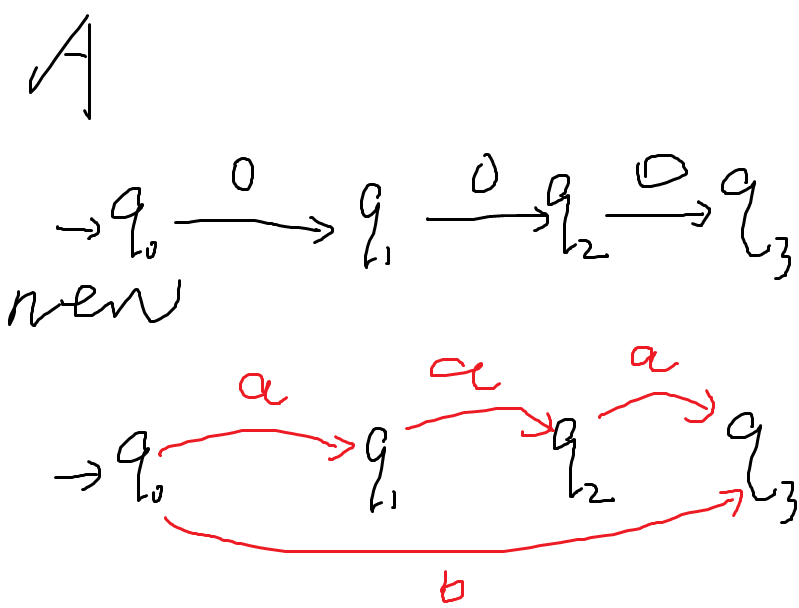
• 正则性还可以在许多种变换后得到保持

最小化问题

• 最小NFA和最短正则都是NP-hard

• 但DFA有最小化的高效（多项式时间）算法

• 思想：我们需要合并一些“等价”状态

  • 第一步：连通性检查，即不可达状态可以直接去掉。然后才是下面的算法

  • 两个状态等价，是指$w$从一个状态读入后被接收等价于$w$从另一个状态读入后被接受

  • 但等价不好检查，我们考虑检查不等价的情况——接受态和非接收态必不等价（注意要考虑到空串！）

  • 考虑列表，横纵轴都是各个状态。然后把接受态和非接收态必不等价用上去作为初始条件（如下，ABCD是状态。假设D是接收态，则D和其他状态都不等价，因此有一排叉）

    

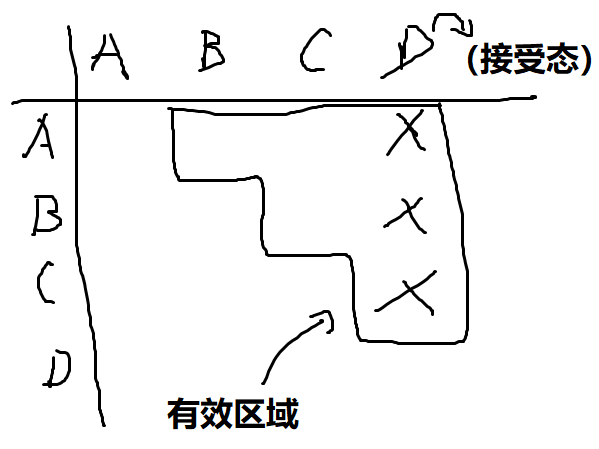
  • 然后一对一对地检查，若暂时无法确定是否不等价就跳过，否则就打叉表示不等价

  • 检查方法：取某字符同时输入待区分的两个状态，若转移后的两个状态不等价，则这两个状态也不等价。（只要有一个字符导致下一跳不等价就能导出不等价）

  • 然后一趟一趟地扫描整张表，若可以确定不等价就打叉，反复多趟直到表在两次扫描后不发生变化，即没打叉的格就是等价的！

  • 然后把等价的状态合到同一个状态里，画边即可（只要指向被合状态中的一个即可加边，根据等价性定义知这样总是可以加边）

  • 显然，复杂度至多$O(n^4)$

  • 最小性证明，假设这样得到的不是最小的（状态不是最小的），于是考虑设置一组串$w_0,w_1,...$，这些串在原先简化的自动机中会到达$q_0,q_1,...$，而更小的自动机中必然会有两个串会到达同一个状态。而这两个串对应的原先简化自动机中的状态是不等价的，于是存在一个串$w$续在这两个串后一个接收一个不接收，但更小的自动机中经过续的$w$必然到达同一状态，产生矛盾。

  • 还可以得到判断语言是否等价：把两个DFA一起同时最小化（得到一张大表），结果一样就是两个语言一样。

  • 正则表达式也可以转成DFA来化简