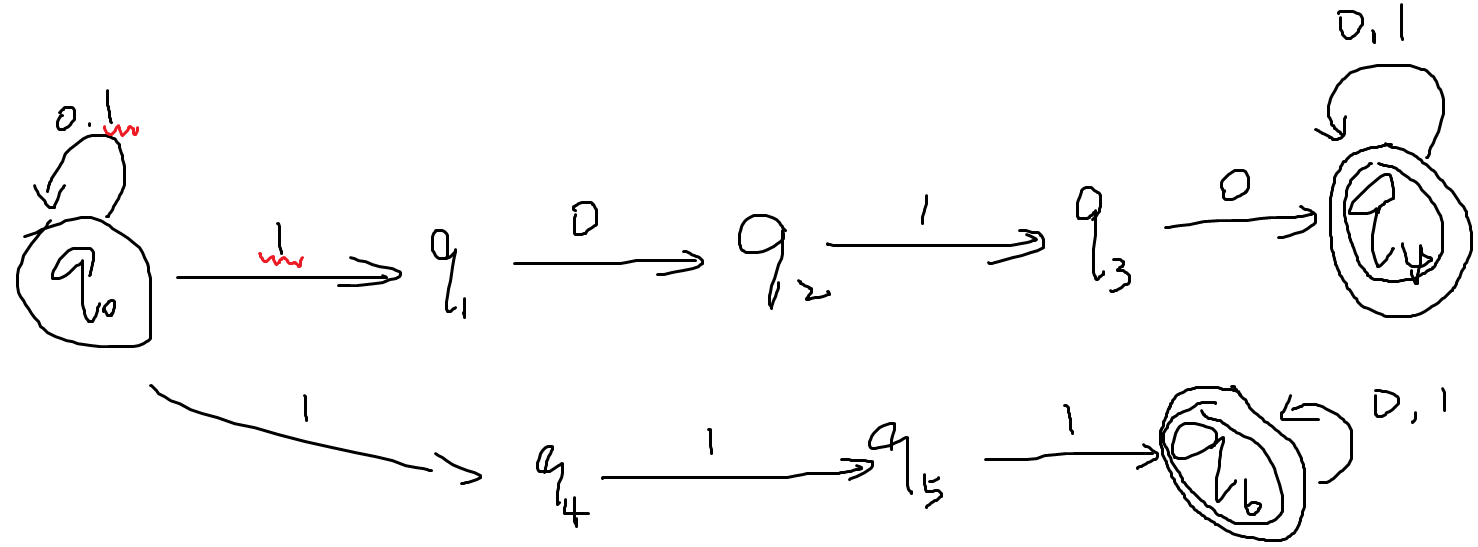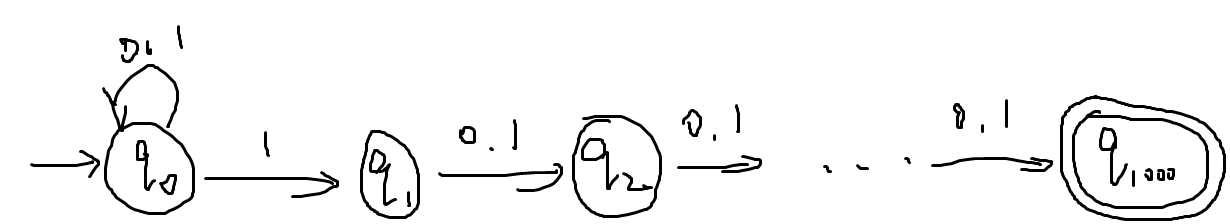有穷自动机

FA，Finite Automata

如交通灯、贩售机等（和数电讲的是同一个DFA），即有穷个状态（点），状态间有转移函数（箭头），有起始和终止状态。

这里的DFA可以接受某些字符串作为输入，通过判别这些串能否到达终止状态来进行计算。

DFA，Deterministic Finite Automata

用 $A$ 代表自动机， $A=(Q,\Sigma,\delta,q_0,F)$
$Q$ ：状态，其中包含一个特殊的起始状态，记为 $q_0$
$\Sigma$ ：字符表。能构成串的字符。字符表大小有限。
- 字符串 $w$ 的长度记为 $|w|$
- $\Sigma^n$ 就是长度为 $n$ 的字符串集， $\Sigma^1=\Sigma$ ，而 $\Sigma^0$ 定义为一个长为0的空串，记为 $\epsilon$
- $\Sigma^*=\Sigma^0 \cup \Sigma^1 \cup...$ 是所有字符串的集合（注意包含空串）
- $\Sigma^*=\Sigma^1 \cup \Sigma^2 \cup...$ 就是 $\Sigma^* - \{\epsilon \}$
$\delta$ ：转移函数， $\delta :Q\times \Sigma \rightarrow Q$
$q_0$ ：起始状态，只能有一个
$F\sub Q$ ：终止状态集，可以有多个
语言 $L$
- 自动机 $A$ 能接受的语言 $L_A=\{\omega\in \Sigma^*|\hat{\delta}(q_0,\omega)\in F\}$
- 其中 $\hat{\delta}(q,\epsilon)=q,\hat{\delta}(q,abc...)=\hat{\delta}(\delta(q,a),bc...)$
- 即能从初始态 $q_0$ 导向 $F$ 的字符串

DFA状态图表示

当然DFA也能画状态图表示，以下给出例子。
- 通常初始态 $q_0$ 前会加个无标签箭头
- 终止状态画双圈，如果指向自身则也要写明其转移状况
- 例如 $\Sigma = \{0,1\},L=\{w|(\#1\space in\space w)\ge 2\}$
- 表示时可以把图画出来，也可以把 $\delta$ 的映射情况全部写出来： $\delta(q_0,0)=q_0,\delta(q_0,1)=...,...$
- 又例：六位密码检查，字符表为0_9，az，A~Z，合法的 $L$ 要求既有字母，又有数字
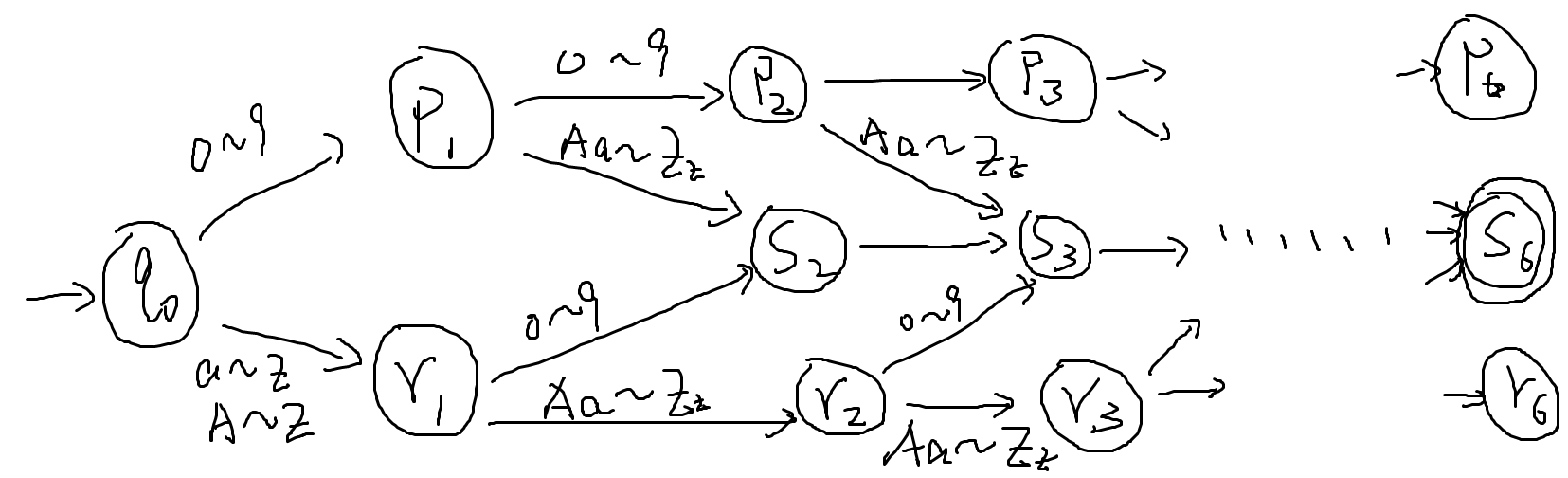
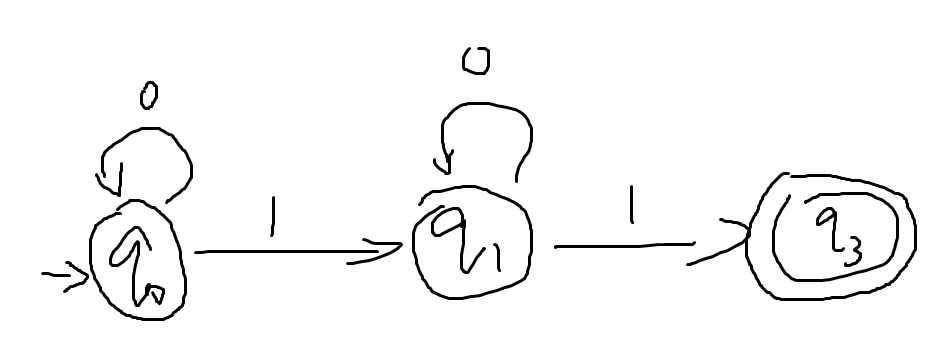
- 又例：字符集0~9，合法 $L$ 是3的倍数（简化起见，允许有前导0）（三个状态是三个同余类）
- 注意：初始态也可以是 $F$
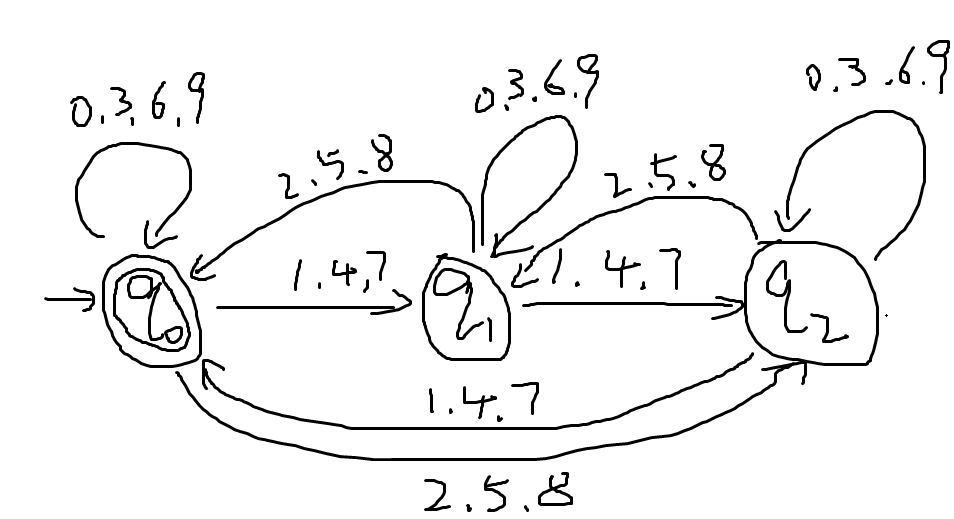
- 又例，合法 $L$ 不是3的倍数，则直接把q1和q2当成接受态（末态），q0不当成末态即可
- 定理 $L=L(A)$ 是A中合法的语言， $\bar{A}$ 是 $A$ 的 $F$ 关于 $Q$ 取补后形成的新自动机，则 $L(\bar{A})=\bar{L}=\Sigma^*-L(A)$
- 反过来说，一个语言会被某个自动机接受，则该语言的补也会被某个自动机接受（自动机对补封闭）
- 又例：字符集 $\{0,1\}$ ，合法语言要包含"1010"子串
- 可以写成 $L=\{w\in \{0,1\}^*|w=a1010b,a,b\in\{0,1\}^*\}$
- 此例子当然可以画DFA，但也可以引出NFA
除此之外当然也能列表表示。

NFA，Non-Deterministic Finite Automata

和DFA最大的区别是转移映射是一对多的。

总可以转换成DFA（随后会证明NFA和DFA能表示的语言是完全一样的），但有时比DFA简洁

$A=(Q,\Sigma,\delta,q_0,F)$
$\delta:Q\times \Sigma \rightarrow 2^Q$ （映射到一组状态上）
$\hat{\delta}(q,abcd...) = \cup_{p\in\delta(q,a)}\hat{\delta}(p,bcd)$ （类似BFS）
$L(A)=\{w\in\Sigma^*|\hat{\delta}(q_0,w)\cap F\neq \empty\}$ （广撒网，只要有一个猜中了就合法）
用这个解决“1010”子串问题就非常简洁（起始位置读到1时有两种可能，故为NFA）
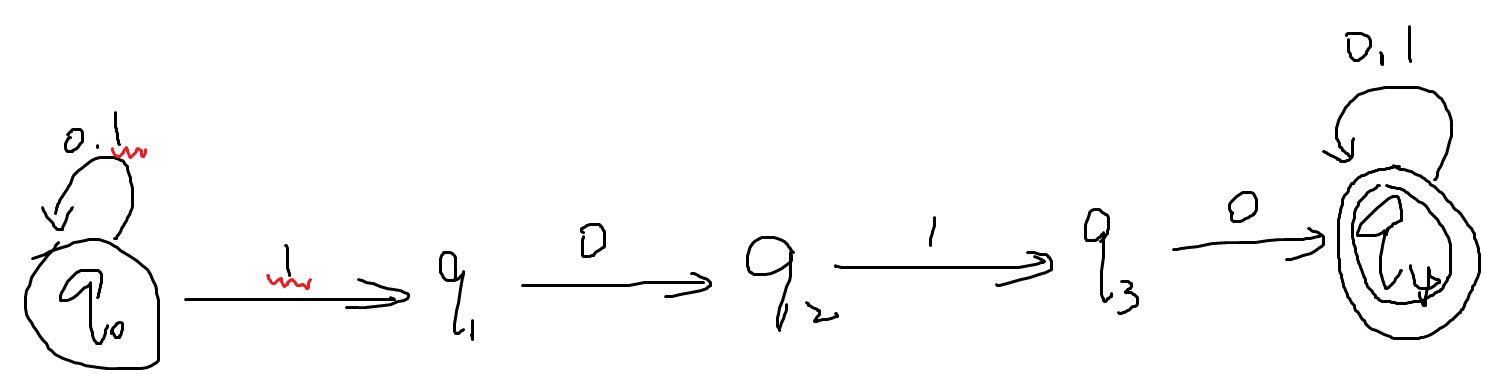
如果要多串也很容易：如要求包含“1010”或“111”，则如下所示（几乎是自动机对并封闭的证明，这用DFA证起来很麻烦）
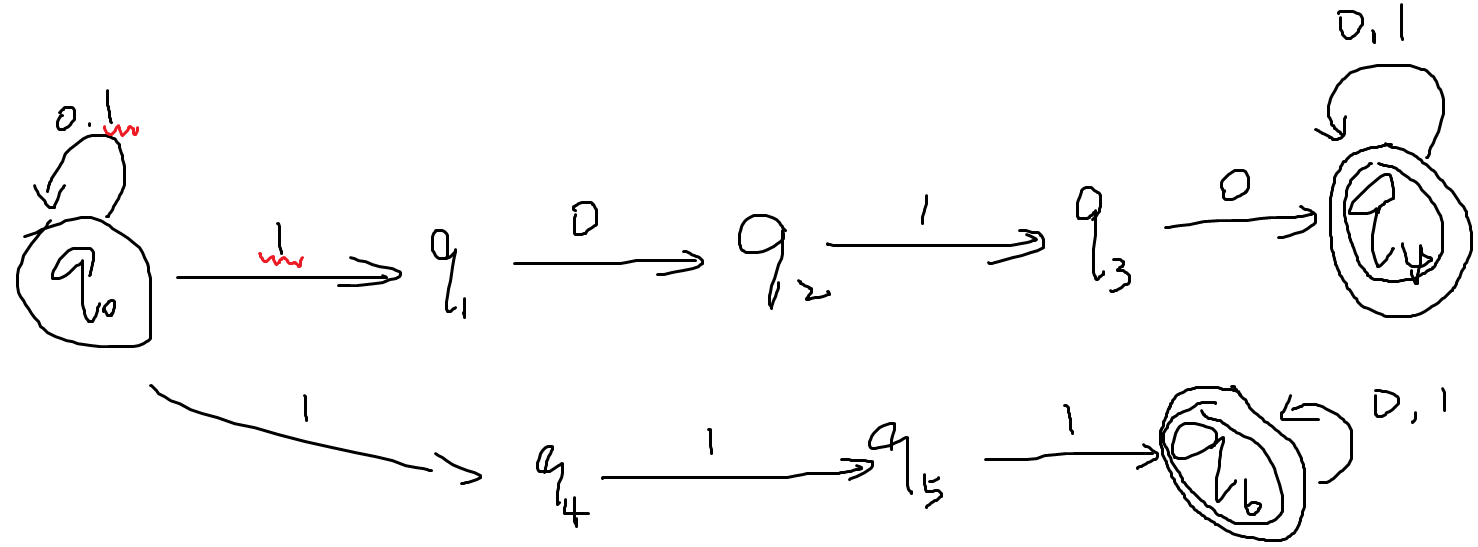
定理 $L_1$ ， $L_2$ 都各自有自动机能识别，则二者之并也有自动机能识别
定理 NFA和DFA能接受的语言其实是一样的，即某语言能在某种自动机中合法，则存在另一种自动机也让这种语言合法。
- $\{L(A)|A\space is \space a\space DFA\} = \{L(A)|A\space is \space a\space NFA\}$
- 显然DFA能算的东西NFA也能算（没有猜测步骤的NFA）
- 关键是反过来——用子集构造法
- 假定 $A=\{Q,...\}$ 是一个NFT
- 则构造相应的DFT $\widetilde{A}$ ，令其状态 $\widetilde{Q}=2^Q$
- 新自动机的终止态就是所有包含原终止态的状态
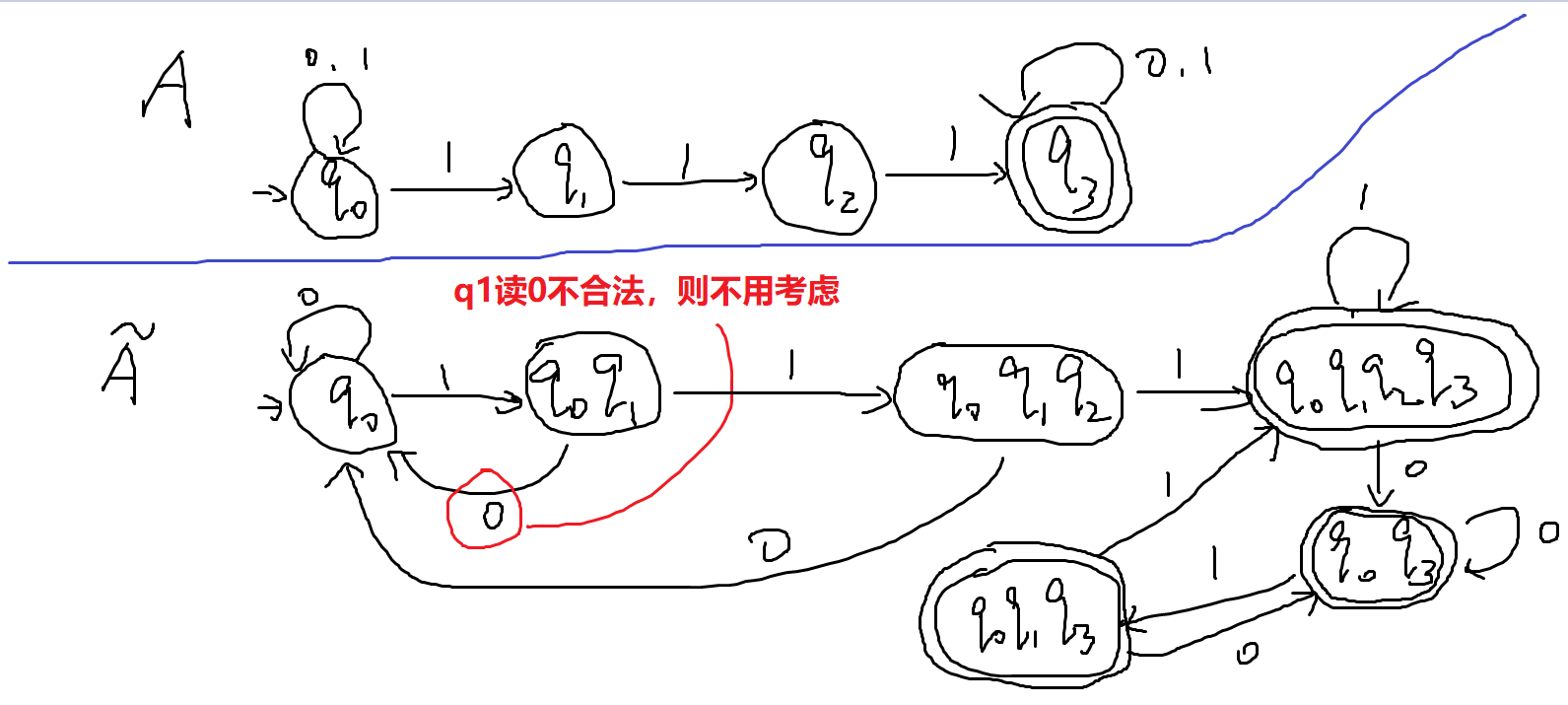
- 当然，这样得到的DFA未必是最简的（如上面DFA的三个末态其实可以合成一个）
从可计算性来讲，NFA相比DFA没优势；NFA的优势是计算效率高（NFA展开成DFA有可能真正需要的状态会增加指数多个（因为是子集操作），因此NFA的加速能力可以达到指数级）
- 如：合法语言为 $\{|w=a1b,a\in\{0,1\}^*,b\in\{0,1\}^{999}\}$ ，即倒数第1k位为1
- NFA如下（注：如果终止态没有向外的箭头则表示到达终止态后若还有输入则自动拒绝）：
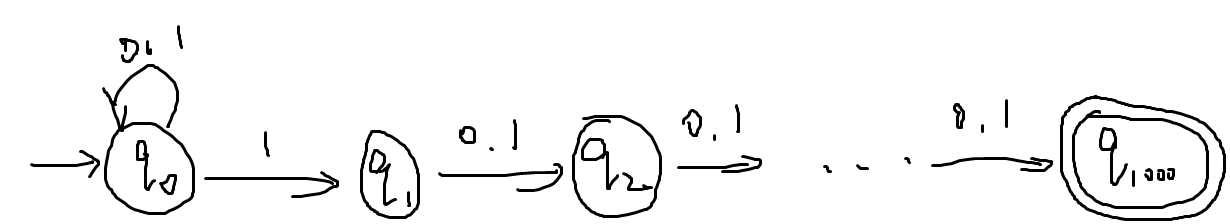
- 注意：不能用子集构造来说明！因为这样得到的DFA未必是最简的！
- 考虑证明： $\forall DFA,|Q_A|<2^{1000}$
- 我们考虑输入0000…0000,0000…0001,…,1111…1111，每个串长都是1000
- 则总共有 $2^{1000}$ 个输入，但状态比这个少，则必然有两个串落在同一个状态上
- 考虑把这两个串从右向左看第一位不一样的位置指出来（必定存在）
- 这个位置右边不会超过999位
- 假设右边不足999位，则在两个串右边同时补零直到补齐到999位
- 则被补齐的两个串居然会落到同一个状态上，且这个状态以后都相同，因此会到达相同的末态
- 但补齐后，二者从右数第1000位就是那个不一样的位置，因此二者的末态应该不同，这就矛盾了
- 当然，其实这里的NFA的状态数是1001，仅仅只是做到 $n$ 和 $2^{n-1}$ 的程度，其实有别的例子可以做到 $n$ 和 $2^n$ 的程度

第三视点

计算理论1

有穷自动机

DFA，Deterministic Finite Automata

DFA状态图表示

NFA，Non-Deterministic Finite Automata