现代第三章(2)：结构分解、标准形、实现问题

简介能观能控分解、Kalman分解、能控/能观标准形、最小实现和结构不确定性等概念，是能控能观性的第二部分。

结构分解

能控状态分解

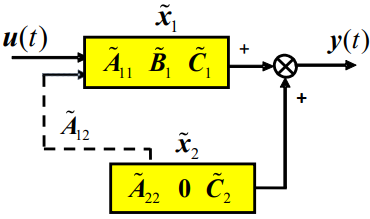
对不完全能控的系统，总是存在非奇异变换T使得:

1. 系统矩阵变成2*2的分块上三角矩阵，上半部分维数等于能控性矩阵的秩（记为r）；
2. 输入矩阵下半部分变为0，上半部分不全为0。即：

$\tilde{\boldsymbol{x}}=\boldsymbol{T}^{-1} \boldsymbol{x}=\left[\begin{array}{l} \tilde{\boldsymbol{x}}_1 \\ \tilde{\boldsymbol{x}}_2 \end{array}\right]_{n-r}^r, \tilde{\boldsymbol{A}}=\boldsymbol{T}^{-1} \boldsymbol{A T}=\left[\begin{array}{cc} \tilde{\boldsymbol{A}}_{11} & \tilde{\boldsymbol{A}}_{12} \\ 0 & \tilde{\boldsymbol{A}}_{22} \end{array}\right]_{n-r}^r \quad \tilde{\boldsymbol{B}}=\boldsymbol{T}^{-1} \boldsymbol{B}=\left[\begin{array}{c} \tilde{\boldsymbol{B}}_1 \\ 0 \end{array}\right]_{n-r}^r \quad \tilde{\boldsymbol{C}}=\boldsymbol{C} \boldsymbol{T}=\left[\begin{array}{ll} \tilde{\boldsymbol{C}}_1 & \tilde{\boldsymbol{C}}_2 \end{array}\right]$

$(\widetilde{B}_1 \neq 0)$

其框图表示为：

传递函数性质

r*r子系统$\Sigma(\widetilde{A}_{11},\widetilde{B}_1,\widetilde{C}_1)$的传递函数和原系统的传递函数阵相等。

Pf. 直接计算即可。

子系统能控性

r*r子系统是能控的。

Pf. 变换后的系统的能控性矩阵为

$\tilde{\boldsymbol{Q}}_k=\left[\begin{array}{cccc} \tilde{\boldsymbol{B}}_1 & \tilde{\boldsymbol{A}}_{11} \tilde{\boldsymbol{B}}_1 & \cdots & \tilde{\boldsymbol{A}}_{11}^{n-1} \tilde{\boldsymbol{B}}_1 \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} \end{array}\right]_{n-r}^r$

其与变换前的能控性矩阵通过一个非奇异变换联系，因此秩也是r。而其下n-r行都是0，因此其上r行组成的子矩阵的秩就是r。

利用Caylay-Hamilton定理可知，$\widetilde{A}_{11}^{i}$总是可以用$I,\widetilde{A}_{11},...,\widetilde{A}_{11}^{r-1}$（注意$\widetilde{A}_{11}$就是r*r的方阵），因此上r行的前r个块的秩就是r，而上r行的前r块恰好就是子系统的能控性矩阵。

变换矩阵T的构造

1. 选择能控性矩阵的r个线性无关的列构成T的前r列；
2. 任意设置T的剩下n-r列，使得T满秩即可。

能观状态分解

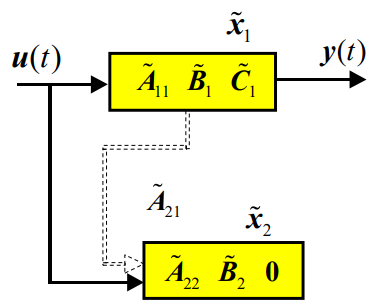
对不完全能观的系统，总存在非奇异变换T使得：

1. 系统矩阵变成2*2分块下三角矩阵；
2. 输出方程右n-r行全部为0，即：

$\tilde{\boldsymbol{A}}=\boldsymbol{T}^{-1} \boldsymbol{A} \boldsymbol{T}=\left[\begin{array}{cc} \tilde{\boldsymbol{A}}_{11} & 0 \\ \tilde{\boldsymbol{A}}_{21} & \tilde{\boldsymbol{A}}_{22} \end{array}\right]_{n-r}^r \quad \tilde{\boldsymbol{B}}=\boldsymbol{T}^{-1} \boldsymbol{B}=\left[\begin{array}{l} \tilde{\boldsymbol{B}}_1 \\ \tilde{\boldsymbol{B}}_2 \end{array}\right]_{n-r}^r \quad \tilde{\boldsymbol{C}}=\boldsymbol{C} \boldsymbol{T}=\left[\begin{array}{ll} \tilde{\boldsymbol{C}}_1 & 0 \end{array}\right]$

系统框图表示为：

典型构造定理（Kalman分解）

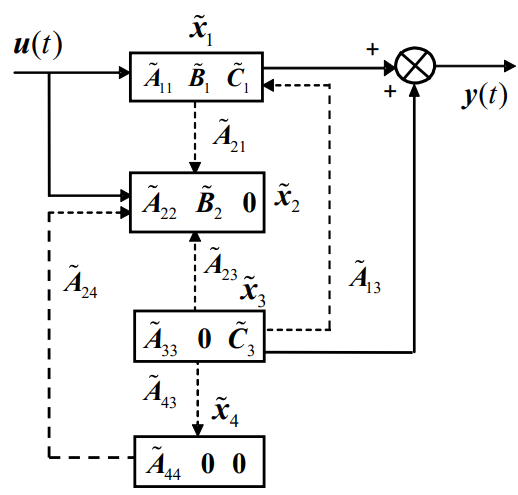
对系统总是可以找到某个非奇异变换$\widetilde{x}=T^{-1}x$，使得状态空间表达式具有如下标准形式：

	且能控	且不能控
能观	$\widetilde{x}_1$	$\widetilde{x}_3$
不能观	$\widetilde{x}_2$	$\widetilde{x}_4$

• 系统的传递函数阵仅由能控且能观的部分决定。
• 系统框图如下所示（虚线和实线并没有本质的区别）

标准形

先针对SISO系统

能控标准形

$\widetilde{A}=\begin{bmatrix}0&I_{n-1}\\-a_n&-a_{n-1}...-a_1\end{bmatrix}$

$\widetilde{B}=[0,0,...,1]^T$

对应的特征多项式：$s^n+a_1s^{n-1}+...+a_{n-1}s+a_n$

性质

1. 能控标准形一定完全能控。
2. 完全能控系统一定可以通过某个非奇异变换变成能控标准形。

**Pf. **1：直接计算能控性矩阵即可。

2：设变换为$x=T\widetilde{x}$，$T^{-1}=[p_1^T,...,p_n^T]^T$，利用$\widetilde{A}T^{-1}=T^{-1}ATT^{-1}=T^{-1}A$得到：

$p_i^T=p_{i-1}^TA$

再利用$\widetilde{B}=T^{-1}B$得到$p_1^T$是能控性矩阵的逆$Q_k^{-1}$的最后一行，即证。

能观标准形

$\widetilde{A}=\begin{bmatrix}0&I_{n-1}\\-a_n&-a_{n-1}...-a_1\end{bmatrix}^T$

$\widetilde{C}=[0,...,1]$

性质

对偶性。考虑本系统的能观性质，只用看其对偶系统的能控性即可。进一步地，若对偶系统能通过非奇异变换$T$变为能控标准形，则本系统能通过$(T^T)^{-1}$变为能观标准形。

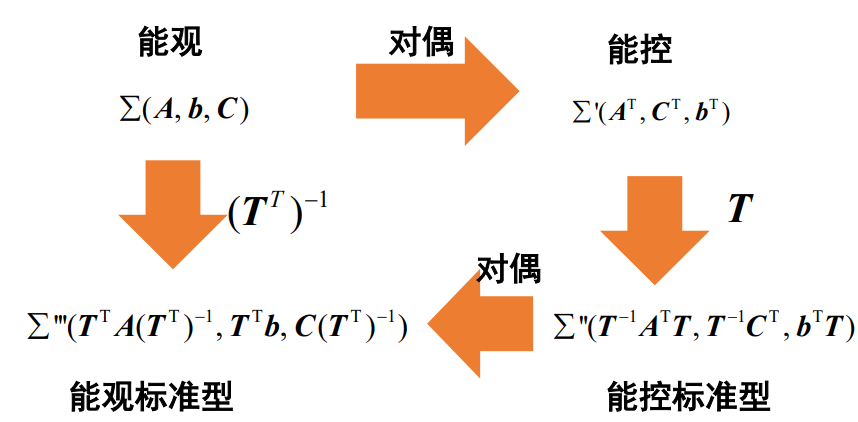
直接给出化为能观标准形的一般方法：

1. 求能观性矩阵的逆$Q_g^{-1}$；
2. 令$p_1$为$Q_g^{-1}$的最后一列；
3. $T=[p_1,Ap_1,...,A^{n-1}p_1]$

实现问题

首先用实验的方法确定其输入输出间的传递函数阵， 然后根据传递函数阵来确定系统的状态空间描述，这就是实现问题。

能控性实现

对SISO的能控性实现在现代第一章已经写过，这里针对MIMO（r维输入，m维输出），因此被实现的是传递函数阵。

1. 确认传递函数阵是真分式，提取公分母到矩阵外，再把分子打开，按照s的幂次分解系数得到如下形式的规范形式：

   $\boldsymbol{G}(s)_{m \times r}=\frac{\boldsymbol{R}(s)}{\phi(s)}=\frac{\boldsymbol{R}_1 s^{l-1}+\boldsymbol{R}_2 s^{l-2}+\cdots+\boldsymbol{R}_l}{s^l+\alpha_1 s^{l-1}+\cdots+\alpha_{l-1} s+\alpha_l}$

2. 则直接代公式得到能控性实现：

   $A=\begin{bmatrix}0&I_{n-1}\\-a_n&-a_{n-1}...-a_1\end{bmatrix}\otimes I_r$

   $B=[0,...,0,1]\otimes I_r$

   $C=[R_l\space R_{l-1}...R_1]$

   其中$\otimes$代表克罗内克积，此实现状态变量数为$lr$，$l$代表极点数。

能观性实现

和能控性实现对偶，但$I_r$要改为$I_m$。（多变量能控性实现和能观性实现的状态维数可能不同。）

关于最小实现

• 对某个传递函数阵，阶数最小的实现称为最小实现

• 某个状态空间表达式是最小实现当且仅当系统能控且能观。因此，最小实现的维数是唯一的。

  证明暂略。

• 对给定的传递函数阵，两个最小实现之间必然代数等价，但若非最小实现，则一般不存在代数等价关系（称为结构不确定性原理）

• 最小实现的构造：

  • 直接法：Ho-Kalman方法
  • 间接法：先求能控/观的实现，然后求能观/控的子系统。