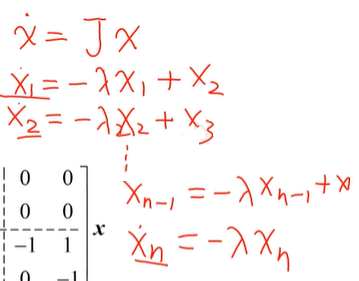现代第三章(1)：能控能观性与对偶性原理

简介能控能观性含义、判据与联系二者的对偶性原理。这是现代控制理论关于能控能观性的第一部分。

能控、能观性定义

以下能控/观和可控/观视为同义词。

在经典控制论中，只有输入-输出关系，因此只要稳定就能控。输出就是被控量，则总是能观。

能控性概念

能控性是指输入$u$控制状态向量（使之能在一段时间后运动到某个状态上）的问题。

能控性只和输入与状态有关，因此讨论能控性只考虑状态方程即可。

定义

对初始时刻$t_0$，初始状态$x_0$而言，若存在有限时刻$t_\alpha>t_0$和$[t_0,t_\alpha]$上有定义的输入向量函数 $u$，使得$x(t_\alpha)=0$，则称该状态是能控的。

如果任意状态都能控，则称该系统是能控的。

注意：

1. 控制向量是一个在$[t_0,t_\alpha]$上有定义的向量函数，而非普通的常向量，因此输入其实是无穷维的。这就解释了为何向量函数的“维数”（指值域的维数）小于状态空间还有可能“能控”。
2. 时刻$t_\alpha$是有限的，因此不能是渐进逼近0，而必须是在$t_\alpha$时刻的状态就等于0。
3. 对状态空间简单平移一下，就可以让终止状态到达任意点去。因此只用考虑如何回到0状态即可。
4. 不考虑无穷远点的能控性。原点则又能控又不能控
5. 定常系统则初始时刻$t_0$可以任意选择。
6. $u$一般约束为时间的分段连续函数。

解析式

• $\dot{x}=Ax+Bu$的解为：

  $x(t)=e^{A(t-t_0)}x_0+\int_{t_0}^t e^{A(t-\tau)}Bu(\tau)d\tau$

• 若在$t_\alpha$能回到原点，则：

  $\mathbf{0}=e^{A\left(t_\alpha-t_0\right)} \boldsymbol{x}_0+\int_{t_0}^{t_\alpha} e^{A\left(t_\alpha-\tau\right)} \boldsymbol{B} \boldsymbol{u}(\tau) \mathrm{d} \tau$

  于是得到$\boldsymbol{x}_0=-\int_{t_0}^{t_\alpha} e^{A\left(t_0-\tau\right)} \boldsymbol{B} \boldsymbol{u}(\tau) \mathrm{d} \tau$

• 因此所有能控的状态$x_0$必然存在相应的$u$满足上式

• 所有能控状态构成状态空间的一个子空间，称为能控子空间。

  证明时需要注意积分限。注意若$t_\alpha$存在，则任意$t'>t_\alpha$也可以使该状态能控.

  此时的输入在$[t_0,t_\alpha]$和取$t_\alpha$时相同，而在此后的时间均为0。由于$t_\alpha$已经回到原点，则各分量导数为0，状态将一直停在原点不动。

  因此，只要是有限个能控状态参与计算，总是可以找到最大的$t_\alpha$，并根据上面的办法把积分限统一到最大值。于是积分的线性直接导出了能控状态的线性。

• 推论：线性非奇异变换和外扰不影响系统的能控性

  有外扰$w$的状态方程为：$\dot{x}=Ax+Bu+Cw$，则$\boldsymbol{x}_0=-\int_{t_0}^{t_\alpha} e^{A\left(t_0-\tau\right)} \boldsymbol{B} \boldsymbol{u}(\tau) \mathrm{d} \tau+W$，$W$是关于外扰$w$的积分项，时间不变就是常值，因此加外扰前后只是做了一个坐标平移而已。

基本判据（补充资料）

• 若能控子空间不能张满整个状态空间，则必然可以在其正交补空间中取出一个非零状态$x_-$，使得$x^T_-x_0=0=-\int_{t_0}^{t_\alpha} x^T_-e^{A\left(t_0-\tau\right)} \boldsymbol{B} \boldsymbol{u}(\tau) \mathrm{d} \tau$。

• 由于求系统能控子空间必然要遍历所有的$x_0$和$u$，因此上式对任意输入$u$成立。若不考虑“几乎处处……”这种情况，则积分恒为零只能导出$x^T_-e^{A(t_0-\tau)}B=0$。

• 因此：函数矩阵 $e^{A(t_0-\tau)}B$的行向量（都是函数）线性无关。（基本判据）

  注意区分“函数线性无关”和“函数在任何时刻的值都线性无关”。这里的函数线性无关是说，不存在常系数使这些函数线性组合起来恒为0值。

  基本判据一般只有理论上的价值。

能达性

若存在输入，使系统能从零初始状态在给定时间后到达给定的末态，则该末态能达。若末态可以是任意状态，则系统在该给定时间上是可达的。

能达性和能控性关系

根据状态方程解，可得能达的状态满足：

$\overline{\boldsymbol{x}}(t)=\int_{t_0}^t e^{A(t-\tau)} \boldsymbol{B} \boldsymbol{u}(\tau) \mathrm{d} \tau$

因此，能达状态和能控状态之间通过双射$-e^{A(t_0-t)}$（指数矩阵必定可逆）一一对应，则有系统能控和系统能达等价。

注意：单就某个状态而言，能控未必能达，能达未必能控。

上述叙述中其实假定了积分限相等，即$t=t_\alpha$。但可以证明，线性时不变定常系统只要在某个$t$时刻有能达性，则该系统给定任意一个有限时间都是可达的。因此$t$总是可以重新选择。

在离散系统中，状态转移矩阵未必奇异，因此可控性和可达性不一致。

从意义上对比，能控性其实是调节问题（误差归零）的可实现问题，而可达性则是跟踪问题的可实现问题。

能观性概念

能观性是指输出$y$反映系统状态向量的能力，即能否通过观察一段有限时间的输出确定初始状态的问题。反过来说，就是初始状态是否能体现在输出中的问题。

能观性和输入无关，因此讨论时直接令$u=0$即可。（或者说由于$u$总是可知的，则强制分量是可计算的常数，因此设为0也不影响能观性的讨论）

定义

对初始时刻$t_0$，若存在有限的$t_\alpha>t_0$，使得在$[t_0,t_\alpha]$上量测的输出能够确定初始状态$x_0=x(t_0)$，则称状态$x_0$在该时间区间上是能观的。

若在初始时刻$t_0$的所有初始时刻都是能观的，则称系统是能观的。

同理，由于一段时间的输出是无穷维的，因此当然可能做到反映有限维的初始状态。

线性连续时间时不变系统：观测的时间只要是有限时间即可，可以随便变化（只要不是只有零测集上的数据，在恢复初始状态上的效果是一样的）

能重构性

若根据$[t_0,t_\alpha]$上输出的观测值，能确定系统在$t_\alpha$时刻的任意状态，则系统在该区间上是能重构的。

线性连续时间时不变系统能观等价于能重构。证明和能控与能达的等价性相似。

能控、能观性判据

能控性判据

模态判据

课上只讨论实特征值的情形。

首先将系统化为约当标准型，然后可以将系统根据不同特征值分成不同子系统，利用以下三种判据中的一种进行判断。（当然，本质上后面的判据包含了前面的情况）

判据1

两两相异特征值，则能控当且仅当标准型的输入矩阵中不含全零的行。

若某行全零，则对应的模态就是不能控的。

证明思路：此时状态变量之间完全解耦，因此可以单独地去看各个单独的分量（模态）。因此只要不是这个分量的微分方程中完全不包含输入，则这个分量就是能控的。

判据2

系统有多重实特征值，且每个特征值几何重数就是1（即每个多重特征值只对应一个约当块），则能控当且仅当约当标准化后，输入矩阵和每个约当块最后（最下）一行对应的行的行元素不全为零

• 代数重数：特征方程重数
• 几何重数：$Ax=\lambda x$的解空间的维数，小于等于代数重数，是约当块的数量。

证明思路：约当块内的状态是相互影响的，因此看约当块中的最后一个即可。

判据3

系统有多重实特征值，且每个特征值几何重数未必是1（即每个特征值可能对应多个约当块），则能控当且仅当各特征值的各约当块的末行对应的输入矩阵的行是线性无关的。

注意 这里只需要在同一个特征值内线性无关即可。判据3包含了判据1&2。

线性无关就可能体现出维数的约束。于是可能出现元素无论怎么变化也不可控的情况。例如：

$\dot{x}=\begin{bmatrix} a&0&0\\0&a&0\\0&0&a\end{bmatrix}x+\begin{bmatrix}?&?\\?&?\\?&?\end{bmatrix}u$

此时无论输入矩阵取何值，系统都是不能控的。

代数判据

模态判据需要计算约当标准型，较为复杂。代数判据在计算上较为简便，且比模态判据更为通用（以上都回避了非实特征值的情形，而代数判据在任何情况下都能用）

系统的能控性矩阵是：

$Q_k=[B,AB,...A^{n-1}B]$。这是一个矮胖形的矩阵，其行数为$n$（状态空间维数）。

系统状态能控的充要条件是其能控性矩阵满（行）秩。

证明：

• 根据Cayley-Hamilton定理，$A$代入其特征方程结果为0，于是$A^n$（乃至更高阶的项）可以表示为$I,...,A^{n-1}$的线性组合
• 因此$e^{A(t_0-\tau)}$也是$I,...,A^{n-1}$的一个线性组合（时间标量作为可变的系数）
• 若能控性矩阵满秩且系统不完全能控，则根据前面已经证明的基本判据，$x^T_-e^{A\left(t_0-\tau\right)} \boldsymbol{B}$恒为0。对此式求到n-1阶导（把$t_0-\tau$看成单个变量）即得$x^T_-e^{A\left(t_0-\tau\right)}A^i \boldsymbol{B},i=0,1,...,n-1$，拼成$x^T_-e^{A(t_0-\tau)}[B\space AB...A^{n-1}B]=0$，和能控性矩阵满秩矛盾
• 若系统能控但能控性矩阵不满秩，则存在非零向量$x^T_-$使得$x^T_-[B\space AB...A^{n-1}B]=0$，即$x_-^TA^iB=0,i=0,..,n-1$，于是进行适当的线性组合（存在性见第二条）可知$x^T_-e^{A\left(t_0-\tau\right)} \boldsymbol{B}$恒为0，于是可知能控子空间的正交补空间维数大于等于1，则不完全能控。

计算时注意：不要去计算$A^2,A^3,...$，而应该迭代式地计算$A^iB=A (A^{i-1}B)$。

有时算出能控性矩阵前若干列发现已经满秩了，则后面的列就不用再算了。

含参系统的判断也是用代数判据更加方便。

非奇异变换

经过变换$x=Tx'$后，$A'=T^{-1}AT,B'=T^{-1}B$。于是变换后$A'^{i}B'=(T^{-1}AT)^i(T^{-1}B)=T^{-1}A^iB$，则能控性矩阵为$Q_k'=[T^{-1}B,T^{-1}AB,...,T^{-1}A^{n-1}B]=T^{-1}Q_k$，两个能控性矩阵的秩是相等的。因此非奇异变换前后系统的能控性保持不变。

能观性判据

根据对偶性原理（见后），能观性问题都能够转化为能控性问题，因此这里省去所有结论的证明。

能观性不受输入的影响，因此可以将输入$u$置为0。

模态判据

判据1

两两相异实特征值，能观当且仅当（化为约当标准型后的）输出矩阵没有全0的列。

如果某列是0，则对应模态根本不参与输出，自然没法观测出其初值。

判据2

有重根但几何重数为1，则约当标准形每个重根每个约当块首列对应的输出矩阵的列不全为0。

首列的理由：只有首列含有第一个状态变量（以下为$x_1$）的信息，而首列的变量就可以递推地得到所有变量的信息

判据3

有重根但几何重数未必为1，则类似能控性，首列线性无关。

代数判据

能观性矩阵为瘦高形矩阵：

$Q_g=\begin{bmatrix}C\\CA\\...\\CA^{n-1}\end{bmatrix}$

系统能观当且仅当能观性矩阵满（列）秩。

非奇异变换

$x=Tx'$变换后，新的能观性矩阵为$Q_g'=Q_gT$。因此非奇异变换能观性保持不变。

对偶性原理

卡尔曼万岁！

对偶性原理 原系统的能控/观性等价于其对偶系统的能观/控性。

对偶系统的定义在前面的文章中已经写过了。原系统的输入（出）数=对偶系统的输出（入）数；原系统与对偶系统的特征方程、特征值相同。

证明：直接用代数判据即可。