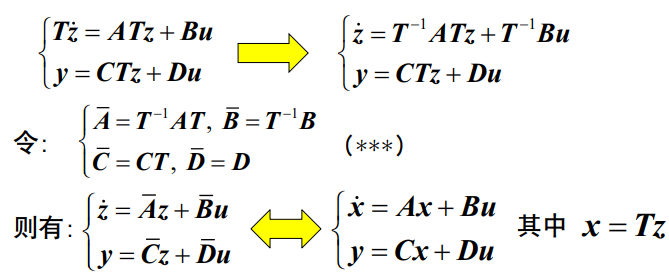现代第一章：状态空间表达式

介绍现代控制理论基本概念：状态、状态空间、状态空间表达式等。

状态空间

状态：揭示动态系统内部运行规律的“特征量”，表示为一组必要而充分的数据。

状态变量：足以完全确定状态的数目最少的一组（关于时间的）变量。

通过状态变量初始值（初始状态）和系统输入可完全确定系统此后的行为。

状态变量的数量$n$就是系统的阶数，通常是系统独立储能元件的个数。

状态向量：将状态变量投射到$R^n$空间中，成为各维度的分量，即得状态向量。状态向量无量纲（量纲可以看成加到了基上）。记为$x=\{x_1(t),...,x_n(t)\}$。

状态空间：以状态变量为坐标形成的$R^n$空间是状态空间。系统状态和状态空间的点相对应。随时间的推移，该点将在状态空间中描绘出一条轨迹（状态轨线）。

状态空间表达式

状态方程：描述状态变量和系统输入的一阶微分方程组。记为$\dot{x}=Ax+Bu$。

输出方程：描述状态变量和系统输出的一阶代数方程组。记为$y=Cx+Du$。

状态空间表达式（状态空间描述）：状态方程+输出方程，记为

$\sum(A, B, C, D)=\left\{\begin{array}{l} \dot{x}=A x+B u \\ y=C x+D u \end{array}\right.$

其中，

$A$：状态系数矩阵/系统矩阵

$B$：输入系数矩阵

$C$：输出系数矩阵

$D$：直接传递矩阵

状态是一种“内因”，经典控制论的“状态”是隐式的，表层只有输入-输出的二元关系。现代控制理论则是输入、输出、状态的三元关系。

能控性、能观性之类就是三元中的二元关系。

传递函数：直接在表达式上Laplace变换，得到系统传递函数矩阵为

$G=C(sI-A)^{-1}B+D$

这个矩阵未必是对角的，因此可以表达MIMO系统不同分量之间的耦合关系。

考试：求逆只要会3*3就成。

组合系统

并联

• 维数要求：输入、输出的维数是相同的（状态数可以不同）
• 结论：系统矩阵就是对角地拼在一起

$\left\{\begin{array}{l} {\left[\begin{array}{l} \dot{\boldsymbol{x}}_1 \\ \dot{\boldsymbol{x}}_2 \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{A}_1 & \mathbf{0} \\ \mathbf{0} & \boldsymbol{A}_2 \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right]+\left[\begin{array}{l} \boldsymbol{B}_1 \\ \boldsymbol{B}_2 \end{array}\right] \boldsymbol{u}} \\ \boldsymbol{y}=\left[\begin{array}{ll} \boldsymbol{C}_1 & \boldsymbol{C}_2 \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right]+\left(\boldsymbol{D}_1+\boldsymbol{D}_2\right) \boldsymbol{u} \end{array}\right.$

• 由上易得：并联传递函数为各子系统传递函数之和。

串联

• 维数要求：前一个输出维数和后一个输入维数相同
• 结论：系统矩阵变成分块下三角

$\begin{aligned} {\left[\begin{array}{c} \dot{\boldsymbol{x}}_1 \\ \dot{\boldsymbol{x}}_2 \end{array}\right] } &=\left[\begin{array}{cc} \boldsymbol{A}_1 & \mathbf{0} \\ \boldsymbol{B}_2 \boldsymbol{C}_1 & A_2 \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right]+\left[\begin{array}{c} \boldsymbol{B}_1 \\ \boldsymbol{B}_2 \boldsymbol{D}_1 \end{array}\right] \boldsymbol{u} \\ \boldsymbol{y} &=\left[\begin{array}{ll} \boldsymbol{D}_2 \boldsymbol{C}_1 & \boldsymbol{C}_2 \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right]+\boldsymbol{D}_2 \boldsymbol{D}_1 \boldsymbol{u} \end{aligned}$

求逆时注意到下三角分块矩阵的特性

• 传递函数：后一个左乘前一个，注意和SISO不一样，次序不能颠倒！

常值反馈

• 设前向通道直接传递矩阵$D=0$，反馈通道只有直接传递矩阵不为0（即没有储能元件、没有状态变量。记其直接传递矩阵为$H$）
• 结论：

$\left\{\begin{array}{l} \dot{x}=(A-B H C) x+B u \\ y=C x \end{array}\right.$

• 传递函数：和SISO情况很相似，但有两种形式。

$G=(I+G_0H)^{-1}G_0=G_0(I+HG_0)^{-1}$

$(I+GH)^{-1}G=G(I+HG)^{-1}$的证明：

$G=(I+GH)G(I+HG)^{-1}=(G+GHG)(I+HG)^{-1}=G(I+HG)(I+HG)^{-1}=G$

动态反馈

• 在常值反馈的基础上，将反馈通道改为只有直接传递矩阵为0即可。
• 结论（2代表反馈通道）

$\begin{aligned} {\left[\begin{array}{c} \dot{\boldsymbol{x}}_1 \\ \dot{\boldsymbol{x}}_2 \end{array}\right] } &=\left[\begin{array}{cc} \boldsymbol{A}_1 & -\boldsymbol{B}_1 \boldsymbol{C}_2 \\ \boldsymbol{B}_2 \boldsymbol{C}_1 & \boldsymbol{A}_2 \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right]+\left[\begin{array}{c} \boldsymbol{B}_1 \\ 0 \end{array}\right] \boldsymbol{u} \\ \boldsymbol{y} &=\left[\begin{array}{ll} \boldsymbol{C}_1 & \mathbf{0} \end{array}\right]\left[\begin{array}{l} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \end{array}\right] \end{aligned}$

• 传递函数：和常值反馈基本一样，把$H$换成新的反馈通道传递函数阵即可

时域描述：能控I型

以下在已知SISO线性定常系统的时域描述（n阶线性常系数微分方程）的条件下转化为状态空间表达式。记微分方程为

$y^{(n)}+a_1 y^{(n-1)}+\cdots+a_{n-1} \dot{y}+a_n y=b_0u^{(n)}+\cdots+b_nu$

注意：设置状态变量的方法有无穷多种（见后），因此这里只是提供了一种方法。

微分方程没有输入的导数

则方程为：

$y^{(n)}+a_1 y^{(n-1)}+\cdots+a_{n-1} \dot{y}+a_n y=u$

直接用经典的方法选择状态变量$x_1=y,x_2=\dot{y},...,x_{n}=y^{(n-1)}$，再注意$\dot{x_n}=y^{(n)}=-a_1y^{(n-1)}-...-a_ny+u$，即有

$\begin{aligned} &{\left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_n \end{array}\right]=\underbrace{\left[\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ \vdots & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right]}_A\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]+\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \end{array}\right] u} \\ &y=\underbrace{\left[\begin{array}{cccc} 1 & 0 & \cdots & 0 \end{array}\right]}_{c^{\mathrm{T}}}\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right] \\ \end{aligned}$

微分方程有输入的导数

$y^{(n)}+a_1 y^{(n-1)}+\cdots+a_{n-1} \dot{y}+a_n y=b_0u^{(n)}+\cdots+b_nu$

此时我们仍沿用上面的状态方程来定义状态变量，即

$x_2=\dot{x}_1,...,x_n=\dot{x}_{n-1}$

$u=\dot{x}_n+a_1x_n+...+a_nx_1$

注意 此时状态变量未必有$x_1=y,...,x_{n}=y^{(n-1)}$

则根据线性系统的性质（其实是多项式卷积的可交换性），马上可以猜出$y$的形式：

$y=b_0\dot{x}_n+b_1x_n+b_2x_{n-1}+...+b_nx_1$

但是输出方程是代数方程，不能有状态变量的导数。但输出方程可以有输入且上式尚未使用，因此直接用$u=\dot{x}_n+a_1x_n+...+a_nx_1$把$\dot{x}_n$代换掉即得（在后面积分器串部分可知，此步等价于假分式变带分式）：

$\begin{aligned} &{\left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_n \end{array}\right]=\left[\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ \vdots & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right]\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]+\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1 \end{array}\right] u} \\ &y=\left[\begin{array}{llll} b_n-a_n b_0 & b_{n-1}-a_{n-1} b_0 & \cdots & b_1-a_1 b_0 \end{array}\right] \boldsymbol{x}+b_0 u \\ \end{aligned}$

这就是能控标准I型（或称控制器规范型、第二可控规范型）。

结构图与表达式

以模拟结构图作为中介，先把传递函数变成某种形式的结构图，然后再将结构图分解、变换成状态空间表达式。

需要在结构图中确定哪些量是状态变量。

基本单元(一阶惯性)的表达式

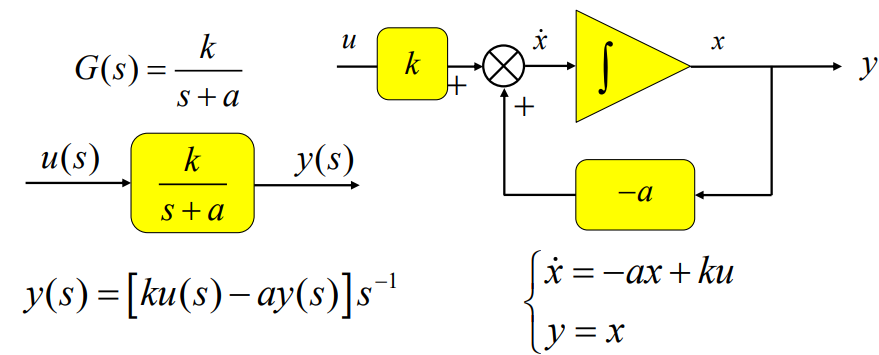
关键点在于：一阶惯性环节的状态变量选为其输出。

串并联分解

将原系统分解成常值块（不含状态变量）和一阶惯性环节（每个一阶惯性环节对应一个状态变量），最后按照表达式的串并联关系连接得到总体状态空间表达式。

注意：积分环节当然也可以看成一种特殊的一阶惯性环节。

实际计算时直接列方程然后写成矩阵形式即可。

部分分式分解：标准型

将传递函数分解为部分分式的和，则可以写成惯性环节的并联形式。

• 当分子无重根（特征值两两相异），则可以写成一阶惯性环节和常值环节（如果传递函数是假分式）的并联，最终系统矩阵是对角矩阵。因此称为对角线标准型或解耦标准型。

• 当分子有重根时，对应的并联支路是高阶惯性环节，最终系统矩阵就是约当标准型的矩阵。因此称为约当标准型。前面的标准型是约当标准型的特殊情况。

  输入、输出系数矩阵和一阶惯性环节的系数在积分器前还是后有关系，但二者互为对偶。（这对系统矩阵没有影响）

纯积分环节：不要反馈的积分器就是了

考试不考重根。

积分器串+常值反馈

设传递函数为$g=\frac{b_0s^n+...+b_{n-1}s+b_n}{s^n+...+a_{n-1}s+a_n}$

第一种：能控I型

1. 假分式变成带分式，然后对真分式部分分子分母同除$s^n$

2. 设出误差量$e=\frac{u}{1+a_1s^{-1}+...+a_ns^{-n}}$

3. 即可很容易地借助反馈画出结构（以下示例为$n=3$）

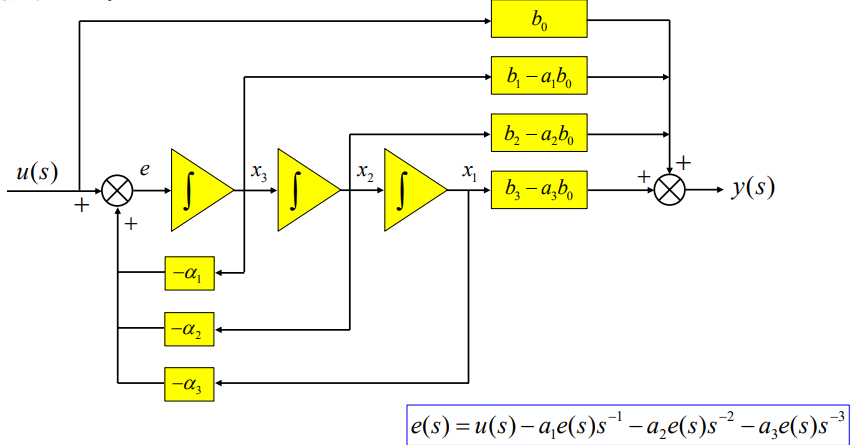
最后表达式写出来就是能控I型（见前）。

第二种：能观II型

直接把传递函数对应的微分方程写成如下形式：

$y=b_0u+s^{-1}(b_1u-a_1y)+...+s^{-n}(b_3u-a_3y)$

于是可以按照秦九韶算法的形式，得到结构图（多层积分法）：

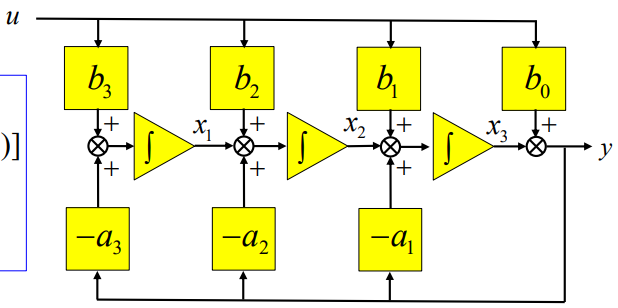
对应的状态空间表达式为：

$\begin{aligned} &{\left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_n \end{array}\right]=\left[\begin{array}{ccccc} 0 & 0 & \cdots & 0 & -a_n \\ 1 & 0 & \cdots & 0 & -a_{n-1} \\ 0 & 1 & \cdots & 0 & -a_{n-2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & -a_1 \end{array}\right]\left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]+\left[\begin{array}{c} b_n-a_n b_0 \\ b_{n-1}-a_{n-1} b_0 \\ \vdots \\ b_1-a_1 b_0 \end{array}\right] u} \\ &y=\left[\begin{array}{lllll} 0 & 0 & \cdots & 1 \end{array}\right] x+b_0 u \end{aligned}$

这就是能观II型，是能控I型的对偶。

一般用 I 型指代能控标准 I 型，用 II 型指代能观标准 II 型。

考试：应该把这两种标准型背下来，用的时候直接代入。

系统等价变化

状态变量组之间总是可以使用一个非奇异的线性变换相互转化：

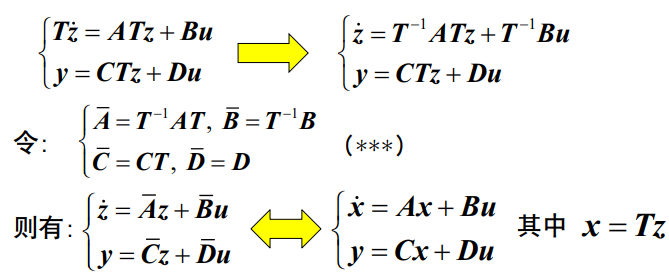
因此：

• 和某系统代数上等价的系统有无穷多。
• 等价的系统之间的特征值是相同的（不变量）
• 还可导出：代数等价的线性系统有有相同的传递函数矩阵
• 求系统的标准型就是做特征值分解，相应的转换矩阵$T$就是特征向量（直接设方程解特征向量）按列排列出的方阵，代入原表达式就是标准型。

考试至多3*3，不考约当标准型

对偶何时也是等价变化？

与原系统对偶的系统为：

$\dot{x}=A^Tx+C^Tu$

$y=B^Tx+D^Tu$

则容易验证：对偶系统的传递函数阵是原系统的转置。因此当系统的传递函数阵是对称阵时，其对偶系统与之等价。特别地，SISO系统总是与其对偶系统等价。（解释了能观II和能控I的等价性）