第七章：非线性系统分析

介绍非线性系统分析的两种经典方法：描述函数法和相平面法。

引入

线性系统：叠加性、齐次性。

分析非线性系统的经典工具主要有描述函数法和相平面法，但他们都没法用于设计。而且这主要是过去没法仿真用的分析方法，现在已经淘汰了。

非线性特点

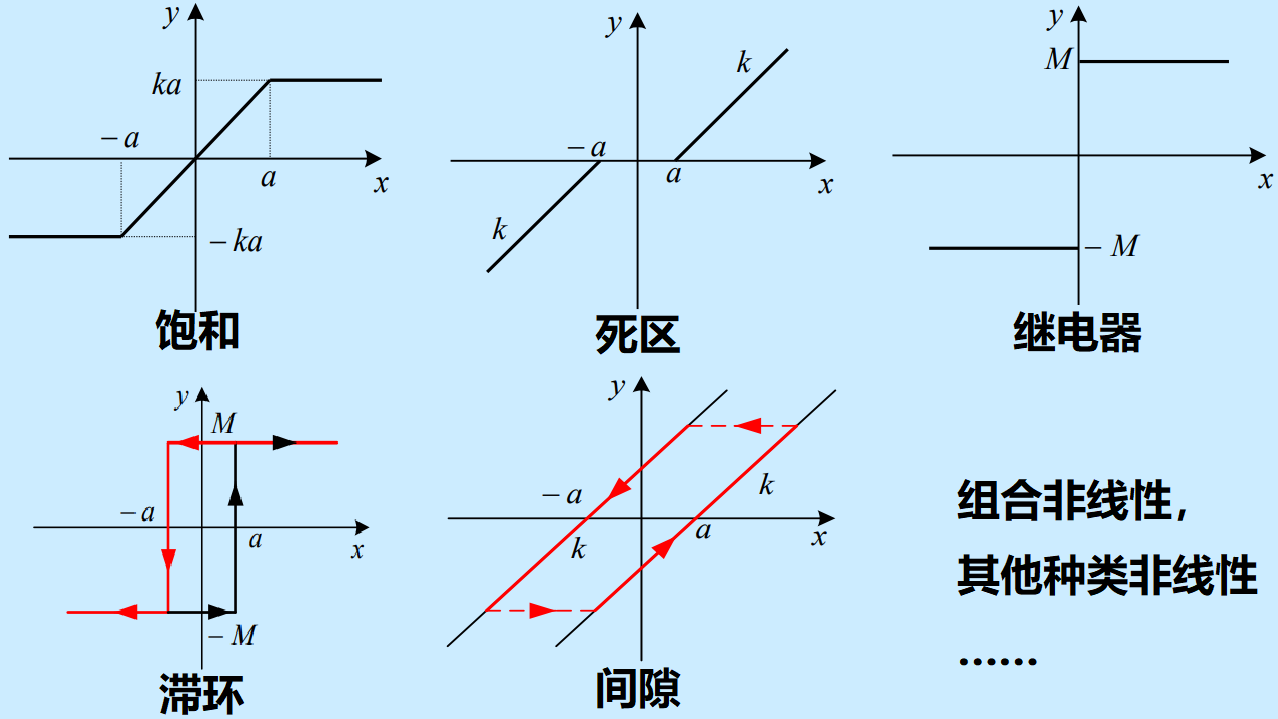
特点

频率-幅值相关性
跳跃谐振：频谱不连续，随频率单调上升/下降会出现类似滞环的情况
自持震荡（极限环）
- 定义：去除外力后，仍存在固定频率和振幅的自持震荡。
- 稳定极限环/不稳定极限环。注意这个稳定和Ляпуно́в稳定性不是一个东西，它只是在说该极限环是否能长期维持下去。只要有极限环，当然就不Ляпуно́в稳定。
分谐波震荡（输入输出频率变化）
Ляпуно́в稳定性依赖于初始条件。因此不能说某个非线性系统整体是Ляпуно́в稳定的，只能讨论某个状态上的Ляпуно́в稳定性
分叉：平衡点的性质和数量和参数相关
混沌：输入的微小变化引起输出的巨大变化

工具

局部线性化
描述函数法
相平面法
Ляпуно́в第二方法
计算机仿真

描述函数法

使用条件

非线性环节可以从线性系统中分离出来，且不能过于复杂。（这主要是出于可行性的考虑）
线性部分具有低通滤波效应，或者说线性部分主要通过低频成分，或者说线性部分是低通滤波器。

于是，我们将输入定为某频率、幅值的正弦波 $X(t)=X\sin\omega t$ ，用输出 $Y(t)$ 的同频率基波分量 $Y_1\sin(\omega t+\phi_1)$ 近似代替输出，则形式上可以确定“传递函数”为 $N=\frac{Y_1}{X}e^{j\phi_1}$ 。

该函数就称为描述函数。它在线性系统频谱分析的框架下近似描述了非线性特性。但需要注意描述函数可以是输入振幅X的函数。

这里讨论的非线性环节其实都是有明确输入-输出关系的非线性函数，和时间无关。因此描述函数并不是 $\omega$ 的函数。

求描述函数

根据非线性环节特性，加输入求输出波形，然后考察其基波分量幅值和相移。

当非线性特性奇对称时，相移为0。

考试不直接计算传递函数，要用到时直接给出。

典型描述函数的负倒数特性

死区、饱和

由于输入输出特性奇对称，因此 $N(X)$ 是实数
$X$ 的取值范围都是自能引发非线性效应开始到正无穷
死区和饱和的负倒数特性都占据的是自 $-1/k$ 到 $-\infin$ 的实轴（ $k$ 就是二者斜的部分的斜率）。只是随着 $X$ 增大，负倒数特性方向不同。
对 $-1/N$ 求导易得：饱和向左、死区向右

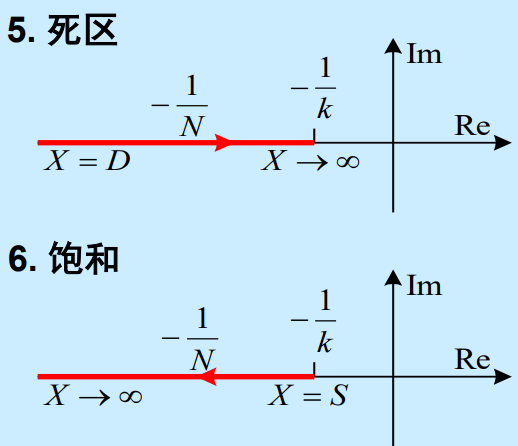
继电器

设继电器的正负值为 $\pm M$ ，则 $N(X)=\frac{4M}{\pi X}$
据此得负倒数特性为负实轴，方向向左

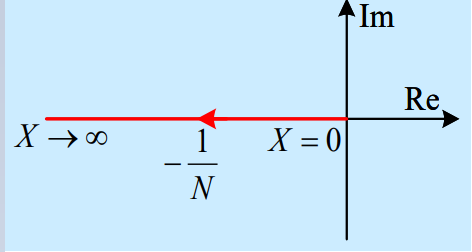
滞环

在继电器的基础上有相移（注意：滞环的每一条曲线都是继电器的平移，因此会有这种结果）
$N=\frac{4M}{\pi X}\exp(-j\arcsin \frac{h}{X})$ ，其中 $h$ 指每条曲线相对继电器的移动量，或者说是横轴交点和原点的距离（即前面图中的 $a$ ）。
$X$ 取值也是从能引起非线性效应的地方开始取，即 $X\ge h$
用欧拉公式展开可知虚部是常数。据此得负倒数特性如下所示

间隙

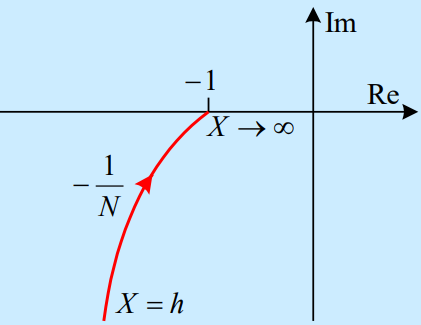
（重点）死区+继电器

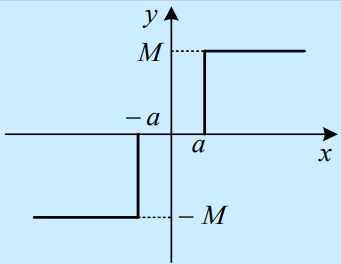
奇对称，描述函数是实数
$X$ 从 $a$ 开始算
$N=\frac{4M}{\pi X}\sqrt{1-(\frac{a}{X})^2}=\frac{4M}{\pi a}\frac{a}{X}\sqrt{1-(\frac{a}{X})^2}\le\frac{4M}{\pi a}\cdot\frac{1}{2}=\frac{2M}{\pi a}$
因此负倒数特性占据 $-\infin$ 到 $-\frac{\pi a}{2M}$ 的一段实轴，且先从负无穷到 $-\frac{\pi a}{2M}$ ，再从该点返回 $-\infin$ 。

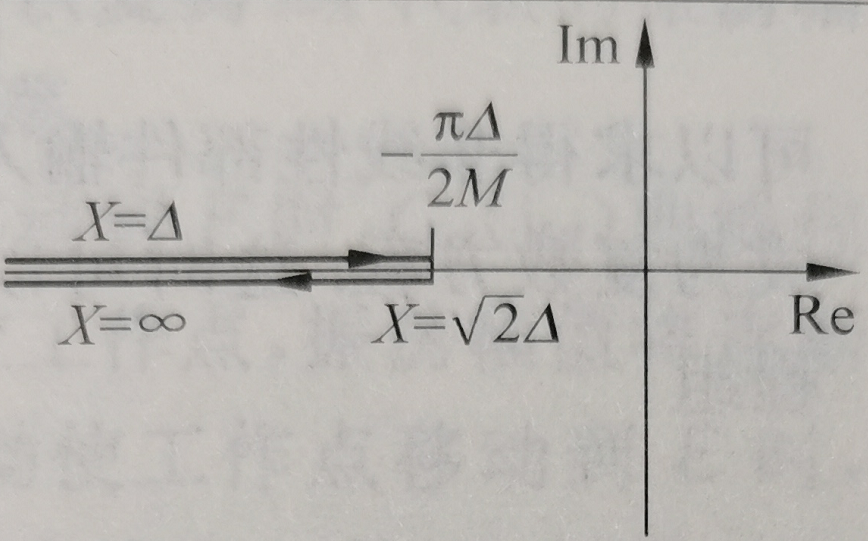
描述函数的合成

串联不能相乘，并联可以相加。

基于描述函数的分析

Ляпуно́в稳定性

直接使用Nyquist准则，单位负反馈下闭环特征方程可以等价地改写为 $G(j\omega)+\frac{1}{N(X)}=0$ ，因此直接把“绕-1旋转……”改成“绕 $-\frac{1}{N(X)}$ 旋转……”即可。
当然， $\frac{1}{N(X)}$ 随 $X$ 变化而变化，当当前的 $X$ 使得系统不稳定时， $X$ 就会继续增大。因此整个系统的稳定性应该看 $X$ 最终停留的位置处的稳定性。

简化：通常假设这里的线性环节 $G$ 是最小相位系统，即有开环不稳定极点数=0.则稳定性就看** $G$ 能否把 $-1/N$ 包在内部**：

注意：考试很可能考非最小相位系统。

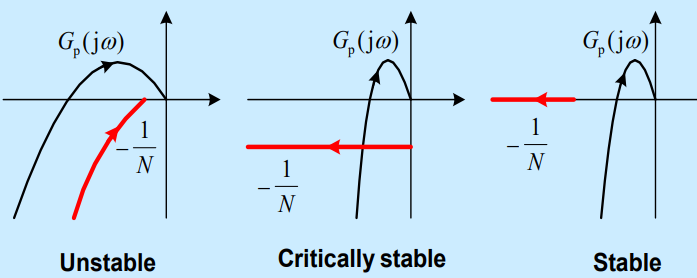
其中“临界稳定”就是自持震荡（注意：稳定和不稳定的自持振荡都叫自持震荡，即使不稳定的自持震荡没法“自持”）。

自持振荡

线性部分的Nyquist曲线和非线性部分的负倒数特性曲线交点是自持震荡，交点位置决定了震荡频率和振幅
- 直接分实、虚部求解闭环特征方程即可得到这两个值。注意利用一些几何条件（如交点在实轴上）
自持震荡稳定性：假定震荡幅值 $X$ $X$ 有微小扰动，观察工作点是否能回到交点上。
- 在上述“简化”假设中，负倒数曲线向左稳定，向右不稳定
- 能实际存在的只有稳定自持震荡

注意：分析自持振荡时可以假设输入为0，有时可以用这个来确定“原系统”的传递函数（见pptP65，这里解出的是 $\dot{x}-x$ 整体，最后还要把 $x$ 本身解出来）

总体流程：
- 求描述函数
- 定负倒数特性作图
- 画对象的Nyquist图
- 看交点、稳定性等

相平面法

两个相变量（其中一个是另一个关于时间的导数）构成平面，每个初值定一个轨迹，一组轨迹形成相平面图。

普通点：沿轨迹运动方向唯一，即非奇点。
奇点： $\dot{x},\ddot{x}$ $\overset{x}{˙}, \overset{x}{¨}$ 均为0，没法得到方向，即不动点。
- 孤立奇点：邻域中没有其他奇点。
- 还是有必要写出斜率的通式，方便后续分析。

性质

运动方向：上半平面向右，下半平面向左
交横轴处总和横轴垂直（ $\dot{x}=0$ ）
奇点总是在横轴上（ $\dot{x}=0$ ）

绘制相轨迹

解析法：硬算

注意公式 $\ddot{x}=\dot{x}\frac{d\dot{x}}{dx}$

$\ddot{x}=\frac{d}{dt}(\dot{x})=\frac{d}{dx}(\dot{x})\dot{x}=\dot{x}\frac{d\dot{x}}{dx}$

警告极限环不依赖于初值，而是总是从任意初值收敛到这个自持振荡处！因此“中心点”不是极限环。

图解法
- 等倾线法：解切向相同点组成的曲线。
  - 先把 $\ddot{x}$ 用上面的公式消去，并固定 $\frac{d\dot{x}}{dx}=\alpha$ ，于是变成一个代数方程；
  - 然后解出 $l(x,\dot{x}|\alpha)=0$ ，这就是斜率 $\alpha$ 对应的等倾线方程。
  - 一堆等倾线就给出了轨迹的方向场，有方向场就能近似画出相轨迹
- Delta法（不考）：不用线段而是用小椭圆弧链接。只用确定小椭圆弧的圆心在哪儿，半径当然就是连线。
更好的办法：对奇点分类，然后画草图
更更好的办法：：计算机仿真

奇点分类

针对二阶系统 $(\ddot{x},\dot{x})=f(\dot{x},x)$ $(\overset{x}{¨}, \overset{x}{˙}) = f (\overset{x}{˙}, x)$
- 先求出奇点（即 $f=0$ 的点）
- 然后求奇点处的 $Df$ ，根据其特征值对奇点分类

复根			实根
Re<0	Re=0	Re>0	均负	均正	一正一负
稳定焦点	中心点	不稳定焦点	稳定节点	不稳定节点	鞍点

节点：汇集的两条线的斜率看两个特征根，原点附近时靠近绝对值小的特征根对应的渐近线

极限环

和初始条件无关且封闭的相平面上的曲线。

重点 PPTp101

不要用书上过于复杂的做法，原点是奇点时去掉高次项可能直接得到特征方程，不是原点时就要平移到原点上。

分片线性系统

一种线性系统切换带来的非线性系统。适合用相平面。

（更复杂的非线性相平面方法就不好弄了）

先考虑二阶线性系统（即没有切换）的相平面法
- 将闭环传递函数化为时域的微分方程
- 还需要知道输入信号的具体形式
- 初值：用物理分析或初值定理（注意初值定理的适用条件）
  - 当某个值不满足初值定理条件，则可以看看相关变量中是否有可求初值的，然后间接解出。
  - 举例：下图中若E的初值没法求，可以通过R、C的初值间接得到。
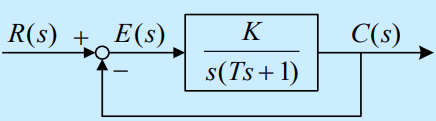
- 求极点：一、二阶导为0消去，剩下的解方程即可
- 特征方程可能已经有了，不一定每次都求矩阵。注意坐标变换把极点移到原点方便。
- 于是即可绘制相平面、相轨迹
- 没有奇点就画等倾线等（用老办法），可能需要分类讨论参数
分片线性：切换时变方程即可（多半不考）
- 实奇点、虚奇点：奇点是/否在对应分片中。
- 滞环处理：正好按照纵坐标（ $\dot{e}$ ）来划分区域
- 不管原系统多复杂，使用的变量通常都选择误差 $e$ 。这样相曲线可以反映静差、超调等时域特征。
- 注意区别画相轨迹和画某点出发的相轨迹
极限环（多半不考）
- 常出现的情况：稳定虚奇点+不稳定实奇点，或两个不稳定区域相邻。
- 从相平面图里直接可以看出振幅的几何意义（到x轴投影中绝对值最大的点）
- 具体算振幅、周期：解微分方程（可以借助L变换，随意设一个环上的点为t=0时刻，然后解超越方程）
- 比描述函数法准

第三视点