第六章：校正

主要介绍单位负反馈系统的串联校正方法：超前校正、滞后校正、超前-滞后校正。不涉及反馈校正。

提纲挈领

• 系统性能的三个主要方面：
  • 稳定性（裕量）
  • 快速性（时间常数+阻尼系数、剪切频率）
  • 准确性（静差、各个误差系数）
• 给定系统的性能达不到要求，就需要加入人为设计的控制器环节改善系统性能（校正）。
  • 串联校正：控制器加在前向通道上。
  • 反馈校正：控制器加在反馈通路上（无通用设计方法）。
• 各个性能指标之间存在冲突。
• 分析方法选择：根轨迹/频率响应
  • 当给出阻尼系数、时间常数、误差系数要求时使用根轨迹。可以用阻尼系数和时间常数得到闭环系统的目标极点。
  • 当给出裕度、剪切频率、误差系数要求时使用频率响应。

超前校正

（以下图源均为课程PPT）

目的：改善稳定性和动态性能

根轨迹法

$G_c(s)=K_c\frac{s+\frac{1}{\alpha T}}{s+\frac{1}{T}}=K_c\frac{s-z_c}{s-p_c},p_c/z_c=\alpha>1$

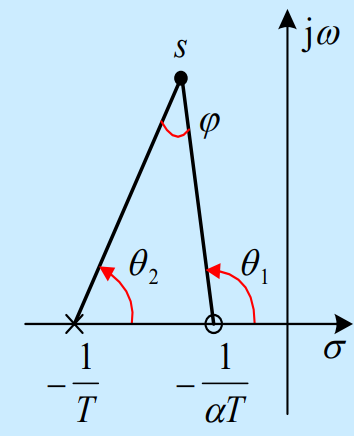
根轨迹如上图所示，则超前环节提供的幅角增量为$\theta_1-\theta_2>0$，因此使得系统相角增大，整体超前，根轨迹左移。

设计步骤

以下的“设计步骤”都是针对考试的最简方法，实际设计未必这么干。

1. 用控制器的零点来消去对象装置最靠近原点的极点（原点除外）。
2. 确定目标极点位置，根据闭环特征方程解出极点和根轨迹增益。

（这种方法没法直接控制静差。如果不达标就再加一个滞后环节。如果误差系数已经定死了且不能再加滞后，则1.中不能自己选零点，而需要根据误差系数、闭环特征方程（幅值条件、相角条件）三个方程解三个未知数）。

注意：对于二阶系统，极点的位置可以通过根轨迹的对称性直接得到，这样上面只用算根轨迹增益，更简单。

频率响应法

• 频率响应形式：$G_c(s)=K_c\frac{1+\alpha Ts}{1+Ts},\alpha > 1$

• Bode图（下图以$K_c=1/\alpha$为例）：

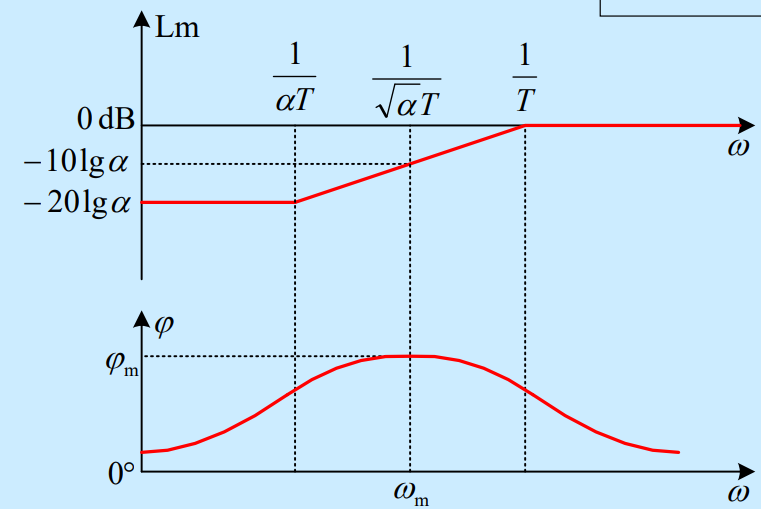
可见其为HPF。易证最大超前角取在两个转折频率的几何平均处（$\omega_m = \frac{1}{\sqrt{\alpha}T}$）

• Nyquist图（下图以$K_c=1/\alpha$为例）：

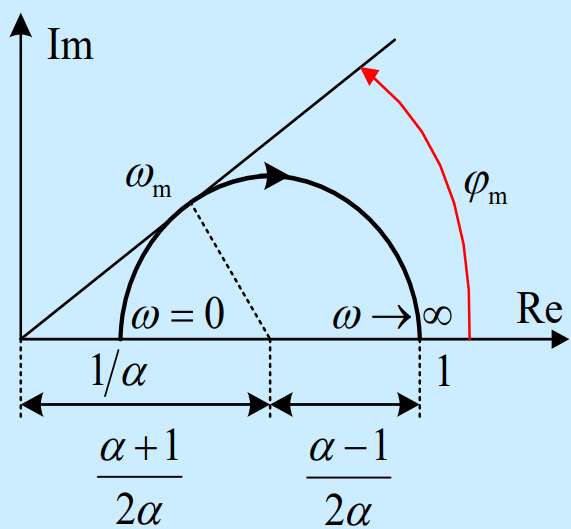
由几何法易得最大超前角$\phi_m$公式：

$$\alpha = \frac{1+\sin\phi_m}{1-\sin\phi_m},\phi_m=\arcsin\frac{\alpha - 1}{\alpha + 1}$$

特别地，当$\alpha=10$时，$\phi_m\approx 55°$。因此如果合适，直接把最大超前角选成55°较为方便。

设计步骤（出题概率低）

1. 根据误差系数确定增益；
2. 假设没有具体给定目标剪切频率，则选择一个离下线不远的频率为目标剪切频率；
3. 计算目标剪切频率处需要多少超前角才能达到相角裕度的要求，然后在此基础上增加5~12°得到最大超前角；
4. 用最大超前角公式得到$\alpha$
5. 让最大超前角落在目标剪切频率上，即$1/\sqrt{\alpha}T=\omega_c$

注意：这种方法最终的剪切频率一般地都不是目标剪切频率。

如果有具体的剪切频率值的要求，则只能放弃约束5.，即先用1~4算出$\alpha,K_c$，再用幅值条件得到$T$。此时剪切频率未必是提供最大超前角的位置，因此裕量够不够就必须小心检验。

滞后校正

目的：改善静差

其滞后角对稳定性和响应速度有负面影响，因此要尽可能将相角下降的部分放到低频。滞后校正通常不太用最小相角和$\beta$的关系式，而是直接用低频的情况确定参数。

根轨迹法

$G_c(s)=K_c\frac{s+\frac{1}{T}}{s+\frac{1}{\beta T}}=K_c\frac{s-z_c}{s-p_c},z_c/p_c=\beta>1$

$K_c\approx 1$

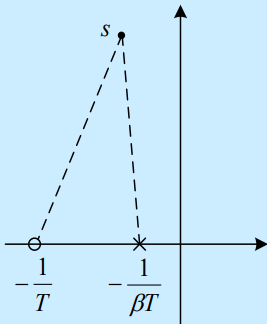
如图所示，滞后校正引入了滞后角，根轨迹右移。

关于系数$K_c$的说明

滞后校正需要在不改变中高频特性的前提下调整静差，这就要求其零点和极点应该相互靠近，从而基本不改变原来的根轨迹（即$p_c\approx z_c$）。记原开环传递函数为$G_0$，则在原来的根轨迹上一点$s_d$有$|G_0|=1$。因此

$|G_0K_c\frac{s_d-z_c}{s_d-p_c}|\approx 1\cdot K_c\cdot 1$

如果要求$s_d$也在加入滞后环节的系统根轨迹上，则上式等于1，于是有$K_c\approx 1$（考试时直接取1即可，不用进一步精确计算）。

当然，调整静差靠的是$z_c/p_c=\beta$，两点又近比值又不为1，于是只能两个点都很靠近原点。

设计步骤

1. 给极点指定一个较小的值（如-0.001）
2. 计算原误差系数，根据目标误差系数求出零点

频率响应法

• 频率响应形式：$G_c(s)=K_c\frac{1+Ts}{1+\beta Ts},\beta > 1$

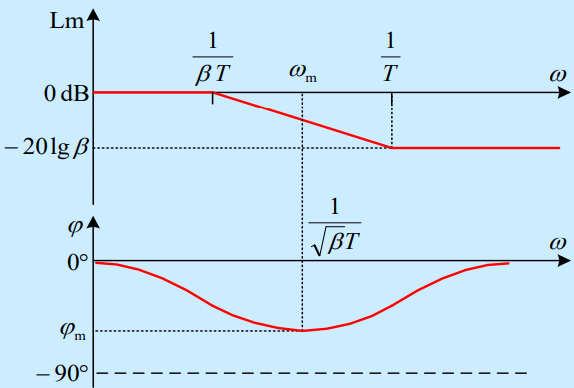
• Bode图（下图以$K_c=1$为例）

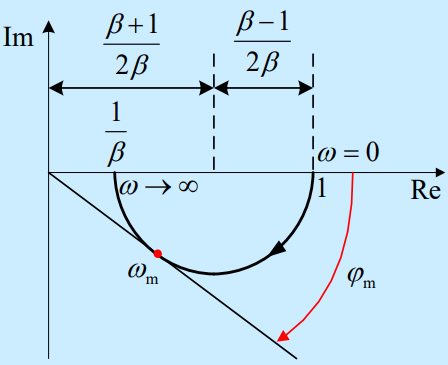
• Nyquist图（下图以$K_c=1$为例）（对滞后校正而言并不重要）

设计步骤

1. 总是令$K_c=1$。（考虑的角度不同，因此略有差别）
2. 先确定一个合适的目标剪切频率 $\omega_c$，这个剪切频率能提供的角度为相角裕量加12°左右。（列$\arctan$方程解）
3. 根据目标剪切频率确定$\beta$。
4. 让滞后的转折频率靠左，远离目标剪切频率。即令$1/T =(\frac{1}{5}\sim \frac{1}{10})\omega_c$即可。

超前-滞后校正

警告：考试时不要用书上的方法，不要限制$\alpha = \beta$！

提示：考试时总是可以先按照超前-滞后装置设计，若超前环节设置完就满足要求就略去后面的滞后环节。

基于根轨迹设计

先对原系统超前校正，再对超前校正后的系统滞后校正。方法和单独设计完全一样。

基于频率响应法设计（出题概率低）

• 先超前再滞后（建议）。做法和前面一样。只是做超前时可以考虑能不能极零点对消一下，再由滞后擦屁股。

• 先滞后再超前。仅当剪切频率已经以固定值给定时可以使用。

  • $\beta$选个比较大的（如10），$1/T$选择$\omega_c/10$，滞后完事。
  • 根据超前角定$\alpha$，再根据剪切频率处幅值为1定超前的$T$。（注意一定会把剪切频率放在超前环节的线性上升段，因此此时超前的折线近似为$\alpha T \omega_c$）