第五章：根轨迹法

介绍根轨迹法以及相关方法。这类方法可以在开环传递函数中某些参数变化时给出相应闭环极点的变化曲线。

导论：对时域法和间接方法的评论

时域法

简明直接，但是计算复杂费时，且难以预测性能随参数变化的影响。

间接方法

Routh判据：易用，但难以判断相对稳定性（其实待定系数也可以），无法直接判定极点所在位置/区域
频域响应法：易用，可以评价相对稳定性，但仍然没法直接判定极点所在位置/区域

根轨迹

Def. 根轨迹就是闭环特征方程的根（闭环极点），作为开环根轨迹增益的函数而形成的图线。

注意：

根轨迹增益不等同于开环增益（开环增益等价于“静态增益”）。

具体而言，“开环增益”的系数是在所有环节写成 $(T_is+1)$ 形式时的整体系数，而“根轨迹增益”则是所有环节写成 $(s-p_i),(s-z_i)$ 形式时的整体系数。

这样做的原因是传递函数的零极点对根轨迹绘制非常重要（见下），因此通常会把传递函数写成零极点显式出现的形式。

根轨迹增益大于等于0得到的是根轨迹，小于0则是补根轨迹，合在一起是全根轨迹。

以下内容未经说明，都是针对根轨迹而言的。

根轨迹的绘制法概要：

对低阶系统可以直接解出根轨迹（例如无零点的二阶系统解出来是十字形）。
对高阶：利用幅值条件、相角条件作草图，进行半定性的分析。
实系数多项式的复根都是共轭对称的，因此只考虑半个平面内的情况即可（但绘制时还是要把完整的根轨迹画出来）

幅值条件、相角条件

假定 $K\ge 0$ （即只看根轨迹），则由闭环的根 $s$ 满足 $G(s)F(s)=-1$ 有：

幅值条件： $|GF|=1$

相角条件： $\arg (GF)=(2k+1)\pi,k\in \mathbb{Z}$

根轨迹上的点和某个根轨迹增益一一对应（即可以用幅值条件确定根轨迹上某点对应的根轨迹增益）。
根轨迹可以仅由相角条件唯一确定（只是如果只有相角条件，则没法知道轨迹上的点和根轨迹增益的对应关系）。

作图法

出发点、终止点、分支数

所有开环极点都是出发点（设有 $n$ 个）；
所有开环零点都是终止点（设有 $m$ 个）；
（通常假设）零点少于极点（ $n>m$ ），则无穷远也是终止点；
（通常假设）零点少于极点（ $n>m$ ），则共有 $n$ （极点数）个分支，有 $m$ （零点数）个分支在零点终止，剩下的终止于无穷远点。

实轴的根轨迹

仅仅取决于实轴上的开环零极点
根轨迹右侧的实零极点总数应该为奇数

简证：在右侧的实零极点带来 $\pm 180°$ 的相角，在左侧的则带来 $0°$ 相角。

终止于无穷远的渐近线

需要确定渐进方向和某个锚定的点（这个锚点通常选择渐进线和实轴的交点）
从无穷远处看，所有环节的相角是相同的。再结合相角条件即可解得这个相角 $\gamma$ ：

$\arg(GF)=(m-n)\gamma=(2k+1)\pi\rightarrow\gamma=\frac{(2k+1)\pi}{n-m}$

这个相角就是渐近线和实轴正方向按逆时针旋转所形成的夹角。
锚点 $(\sigma_a,0)$ 为 $\sigma_a = \frac{\sum p_i-\sum z_i}{n-m}$ 。

证明

$GF=K\frac{\Pi (s-z_i)}{\Pi (s-z_i)}=-1$ 可以转化为 $-K=s^{n-m}+(\sum z_i-\sum p_i)s^{n-m-1}+...$

当 $s\rightarrow \infin$ ，即有：

$(-K)^{1/(n-m)}=s(1+\frac{\sum z_i-\sum p_i}{s}+...)^{1/(n-m)}=s(1+\frac{\sum z_i-\sum p_i}{(n-m)s}+...)$

略去低次项（即省略号内容），再把实、虚部显式写出，即有

$K^{1/(n-m)}(\cos\frac{(2k+1)\pi}{n-m})+j\sin\frac{(2k+1)\pi}{n-m})=\sigma + j\omega + \frac{\sum z_i-\sum p_i}{n-m}$

实部虚部分别相等，立即解出渐近线方程为：

$\omega = (\sigma-\frac{\sum p_i-\sum z_i}{n-m})\tan\frac{(2k+1)\pi}{n-m}$

当 $\gamma$ 为180°时，再求实轴上的锚点就没有意义了。

分离汇合点

分离汇合点一定是闭环特征方程的重根。显然，对多项式而言，其某个根是重根仅当此根处多项式方程的导数为0。

当然，k重根对应0~k-1阶导为0。但绝大多数课内遇到的简单系统都是2重根，因此只有原闭环特征方程及其导数为0两个条件。多于2重根的例子参考《自动控制理论例题习题集》对应章节的某道例题（3重根）。

设 $B,A$ 是（把 $K$ 给去掉的）开环分子、分母，则闭环特征方程为 $A+KB=0$ 。令此式导数为0并把 $K=-A/B$ 代进去即可解出重根。能使 $K\ge 0$ 的点就是根轨迹的分离汇合点。

等价地，也可以由 $K=-A/B$ 对 $s$ 求导得到极值（重根），将局部极值代回 $K=-A/B$ ，能使 $K\ge 0$ 的 $s$ 就是根轨迹的分离/汇合点。（否则是补根轨迹的分离/会合点）

当然，如果该点就在实轴上，则可以直接由实轴的根轨迹分布直接确定，不用代回 $K=-A/B$ 看符号了。但分离/汇合点未必总是在实轴上（虽然这是经常出现的情况）（实系数三次及以下则必然在实轴上）。

考试既不会太难，也不会太简单。因此通常考三阶的情况。

出射角

记极点 $p_r$ 的出射角为 $\phi_{pr}$ ，则可以通过取一个很靠近 $\phi_{pr}$ 的点，利用相角条件：

$\arg(GF)=\sum_i\arg(p_r-z_i)-(a\phi_{pr}+\sum_{i,i\neq r}(p_r-p_i))=(2k+1)\pi$

其中 $a$ 代表 $p_r$ 的重数。由此即可算出出射角（当重数为1时， $k$ 随便取一个值即可）：

$\phi_{pr}=\frac{(2k+1)\pi + \sum_i\arg(p_r-z_i)-\sum_{i,i\neq r}(p_r-p_i)}{a}$

利用对称性，共轭的极点只用算一个其中一个的出射角即可。

入射角

和出射角类似。记重数为 $a$ 的零点 $z_r$ 的入射角为 $\phi_{zr}$ ，则

$\phi_{zr}=\frac{(2k+1)\pi + \sum_i\arg(z_r-p_i)-\sum_{i,i\neq r}(z_r-z_i)}{a}$

与虚轴的交点

令 $s=j\omega$ ，然后联立方程令 $1+GF$ （即闭环特征方程）实、虚部分别为0，从而同时解出 $K$ 和对应的 $\omega$ 。

当然，也可以带着未知量 $K$ 做Routh判据，然后根据第一列全正列式解出交点。但这种方法不如上面的直接法简明，计算量也未必更低。

极点之和的守恒

开环分母高于分子两阶或以上，则开环极点和=闭环极点和。

证明

注意到 $(x-a_1)...(x-a_n)=x^n-(\sum_ia_i)x^{n-1}+...$ 。

一方面，闭环特征方程开环在分母高于分子两阶或以上时，可以写成：

$\Pi(s-p_i)+K\Pi(s-z_i)=s^n-(\sum_ip_i)s^{n-1}+...+K(s^m-(\sum_ip_i)s^{m-1}+...)$

$=s^n-(\sum_ip_i)s^{n-1}+...$

另一方面，设闭环极点为 $a_1,...,a_n$ ，则闭环特征方程可以写成：

$\Pi(s-a_i)=s^n-(\sum_ia_i)s^{n-1}+...$

对比次高次项系数即证。

“不考”

——wl

总体流程（其余的细节不要求）

列出 $GF$ ，开环零极点，特征方程
出发/终止点，分支数
实轴根轨迹
渐近线
分离/汇合点
出射/入射角
虚轴交点

MATLAB使用：调用rlocus即可。MATLAB中表示传递函数的方法参考第四章blog。

应用

定条件稳定性
分析比例控制器
设计控制器：
- （通常）加零点（PD）左移（变快，通常也能减小超调），加极点（PI）右移
- PI正是以右移为代价试图换取（可能更高的）根轨迹增益，从而降低静差。
- 也可以用于PID，一般先设计PD再设计PI（根轨迹对极点极为敏感）

参数根轨迹、根轨迹簇

参数根轨迹

实际问题中，待确定的参数未必是根轨迹增益，因此需要进行转换，变成经典的根轨迹问题。即若需要讨论的可变参数为 $a$ （且 $a\ge 0$ ），闭环特征方程可以变形整理成 $1+aG'(s)=0$ ，则 $a$ 可以变成 $G'$ 开环系统的等价根轨迹增益，此后按照正常根轨迹的方法做即可。

根轨迹其实是参数根轨迹的特例。

根轨迹簇

参数未必只有一个。

如果是两个参数 $K_1,K_2$ ，且闭环特征方程可以写成可分离的形式 $P+K_1Q_1+P_2Q_2=0$ ，就能作根轨迹簇。

令其中一个参数（例如 $K_2$ ）为0，则变成单参数根轨迹问题，先将其根轨迹做出来。
假设 $K_1$ 不变，则特征方程变成 $1+\frac{K_2Q_2}{P+K_1Q_1}=0$ 。因此** $K_2$ 的根轨迹就从第一步中作的根轨迹上由 $K_1$ 确定的某点起始**。不同的 $K_1$ 可以作出从不同点出发的的根轨迹，形成一簇根轨迹。真正的闭环极点就在第二步的这一簇根轨迹上。

有时也需要注意根轨迹是否形成了特定形状（如圆形等）

时延环节和普通环节串联（不考，只给出结论）

基本想法：还是看幅值条件和相角条件。设 $s=\sigma + j\omega$ 代进去即可
出发点：普通环节的极点、所有实部为 $-\infin$ 的点
终止点：普通环节的零点、所有实部为 $+\infin$ 的点
渐近线：所有渐近线平行于实轴
分支数：无穷多
实轴的根轨迹：和普通环节看奇偶一样
分支点：还是求导
虚轴交点：是超越方程，可以数值法/估计/配凑

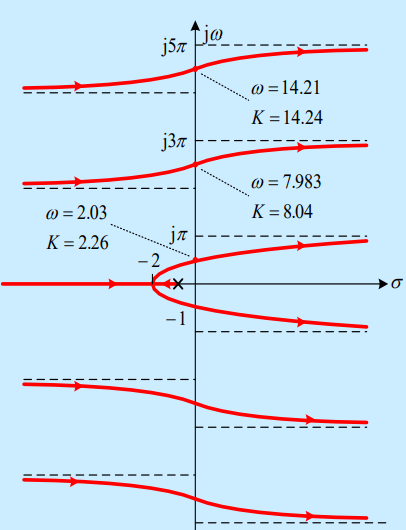
结论：对稳定不利；时延越大，参数稳定的范围越小

在MATLAB中，可以用Taylor展开近似作出其根轨迹。

补根轨迹、全根轨迹

非最小相位或正反馈或要讨论 $K<0$ 的情况使用补根轨迹。

和根轨迹唯一的区别是角度条件变成偶数倍 $\pi$ ！（幅值条件不变）

按：只要都是 $(s-s_i)$ 式的因子没问题，因此不是所有非最小相位都需要特别处理

只有和角度相关的要变：

实轴根轨迹
渐近线
出射、入射角

另外还有两个虽然和角度无关，但还是有所变化的地方：

分离汇合点（计算是一样的，主要是后面验证时要求 $K$ 为负数）
补根轨迹的出发点指 $-\infin$ ，终止点指 $0^-$ ，因此零点是起点，极点是终点

最后，根轨迹+补根轨迹=全根轨迹