第四章：频率响应法

介绍频率响应、Bode图、Nyquist图、Nyquist稳定性判据等内容。

可以证明，对稳定的LTI系统而言，用一定频率的三角信号做激励得到的响应在稳态时也是三角信号，且频率和激励信号相同。而现实中能遇到的信号几乎都能在三角函数基底下进行线性分解（Fourier），因此，如果能够知道系统对各个频率的三角信号的响应情况（即频率响应），那么这个系统对任意信号的响应就都能搞清楚了。从黑箱（或者说辨识）的角度而言，这个系统也就确定了。

因此，频率响应和传递函数一样能完全定义一个系统。事实上，随后将阐明频率响应和传递函数之间的联系。

频率特性函数

由于三角激励的输出也是同频率的三角信号，因此对每个频率而言，只需要两个参数即可确定输出：幅频放大的倍数、相位差。因此，这对应地定义了幅频特性函数、相频特性函数。

定义频率特性函数为这样的复函数：其幅值为幅频特性函数，相角为相频特性函数。

这种定义方式可以和传递函数搭上关系，见下：

和传递函数的关系

传递函数中的复频率 $s$ 直接换成 $j\omega$ ，就得到对应的频率特性函数。

证明：按照定义直接通过频域计算三角激励的响应，再转换回时域看稳态解得证。

由此，可以将频率特性拓展到所有具有传递函数的系统上，而不再要求系统稳定（如果按照原来的定义，不稳定系统没法定义频率特性）。

Nyquist图（幅相频率特性图）

将频率当成隐变量（参数），把某系统幅频特性和相频特性关系在极坐标平面绘出的曲线称为Nyquist图（需要标出频率增加的方向）。这种图具有以下特征：

对称性：将频率 $\omega$ 变为 $-\omega$ ，幅频不变，相频变为相反数。因此对应的两个点关于 $0°$ 轴对称。

所以通常只用画 $0^+\sim +\infin$ 段的曲线即可，在有必要补全时再补全。
当分母阶次严格高于分子时，终点在原点。
当有积分环节时，起点在无穷远点。

注意使用条件。另：也可以通过观察幅频特性得出结论。

示例：一阶惰性环节的Nyquist图是个半圆。

Bode图（对数频率特性图）

幅频特性幅度增益轴、频率轴是对数刻度，但相频特性角度轴不是对数。
一般指幅频、相频两张图（有时也专指幅频特性）
特点
- 正数乘：幅频上下移动，相频不变；负数乘除此外加相角变化180°
- 时间常数变化：（对应的惰性环节）幅、相都左右平移
- 频率特性相乘：幅、相频曲线相加
- 频率特性互为倒数：幅、相频关于对数频率轴对称

典型环节的Bode图

不加说明，均指稳定环节。

比例单元：幅频为绝对值，相频为0°或180°
积分单元 $G(s)=k/s$
- -20dB/dec
- 剪切频率就是系数 $k$
惰性单元 $G(s)=1/(Ts+1)$
- 在拐角频率（ $1/T$ ）处实际的幅值降为最大幅值的 $1/\sqrt{2}$ ，对应（相对的） $-3dB$
- 近似：折线
- 下降部分：-20dB/dec
- 相频：从0°到-90°，关于拐角频率对称
二阶震荡单元 $G(s)=1/(T^2s^2+2\xi Ts+1)$
- 拐角频率：通过约去二次项系数使得二次项系数为1，然后把常数项开方即可
  
  意外地，这里一糊涂很容易犯错👆
- 下降部分：-40dB/dec
- 但是，假如拐角频率附近（按：即谐振频率，通常略小于拐角频率）有个尖峰，则还是要把尖峰画出来，并标出尖峰的高度。
  - 有尖峰条件： $\xi\le 1/\sqrt{2}$
  pf. 幅频特性模的倒数再平方得 $1/|G|^2=(1-\omega^2T^2)^2+(2\xi T\omega)^2$ ；
  
  求导得驻点 $\omega_r=\frac{\sqrt{1-2\xi^2}}{T}$ ；
  
  对应的幅频函数极值为 $|G|_{max}=M_r=\frac{1}{2\xi\sqrt{}1-\xi^2}$ ；
  
  当峰值 $M_r$ 超过1时，就认为有尖峰。据此解出有尖峰条件。
  
  注：需要记住 $\omega_r$ 和 $M_r$ 的公式，以免考试现推，，，
- 相频：从0°到-180°，关于拐角频率对称（注意：不是关于谐振频率对称）
- 考试出题的可能性偏低
微分单元：利用对称性，把惰性环节的结论搬过来就成。
延时单元：幅频是个圆，相频是本来是线性函数，但在对数坐标系就成了指数曲线
一阶不稳定单元（模和稳定的单元一样，只是相角有变化）

小心：不要拿分母的辐角当成整体的幅角
- 最小相位系统：稳定系统，且零极点都在左半平面。因此三个一阶不稳定单元都是非最小相位系统。

复杂系统的Bode图

画频率特性法：若干简单系统相加
求剪切频率：利用折线化，把未知量 $\omega$ 带进（相应线性化的）传递函数里去（这种方法要先确定剪切频率在哪两个拐角频率之间）
在Bode图的基础上画Nyquist图：关键看起点和终点的情况（点位置和切方向是否正确，中间是怎么弯曲的不做要求。）
算Nyquist曲线何处穿越负实轴：令相频函数=180°得到方程（建议写成多个 $\arctan$ 之和的形式，不易出错），两边取 $\tan$ ，再利用和角公式即可得到关于 $\omega$ 的多项式方程。

如果只是判别稳定性，则看剪切频率处的辐角也可以，毕竟剪切频率好算得多。
不是标准形一定要先化为标准形（各基本环节常数项为1），另外注意二阶环节二次项系数要开方写成 $(Ts)^2+...$ 形式。对二阶环节务必考虑是否有尖峰。

注：由于二阶环节的曲线是加到bode图上去的，因此用前面“峰值公式”算出的峰值指的是增量，即峰值频率上的幅值增益并非算出来的峰值。课件中p37这个地方是错误的。

课件p37中还有一个错误：折线法近似后尖峰前的一段其实是在横轴下方（虽然真实幅频曲线确实是在横轴上方：这是渐近折线法近似过度的问题。）
相频特性标准的解算方法是取点列表计算。
最小相位系统的幅频和相频特性有严格对应关系（ $-k\cdot 90°$ ）。非最小相位系统画相频就需要具体分析。

MATLAB ：bode、nyquist（可以设置频段）

在MATLAB中可以使用至少2种方法定义传递函数：
用系数数组表示，如H=tf([1 2 0],[4,5,6])代表 $H=\frac{s^2+2s}{4s^2+5s+6}$

这种方法需要把多项式展开，并且要小心缺项处别忘记写0。

如果要表示多个因子相乘，则可以利用conv函数（但非常不方便，此时建议用方法2）。
用s=tf('s')即可在MATLAB中指定复频率变量，后续可以直接用s写多项式。例如 $H=\frac{s^2+2s}{(s+1)(s+2)}$ 可以写成：
1
2
s = tf('s')
H = (s^2 + 2*s) / ((s + 1)*(s + 2))
在定义传递函数后即可用bode(H)得到bode图。

若希望显示裕量（见后），则可用margin函数取代bode。

同样地，在定义传递函数后可以用nyquist(H)得到Nyquist图。

Nyquist判据

以下总是假设为单位负反馈。

低、中、高频段与时域参数的联系

设开环传递函数为 $G$ ，则闭环传递函数为 $\frac{G}{1+G}$ 。通常情况下有：

低频段 $|G|\gg 1$ ，则闭环频率特性大致为 $1$ ；
高频段 $|G|\ll 1$ ，则闭环频率特性约等于开环频率特性；
中频段则变化较多：若开环的频率特性能等于 $-1$ （幅频 $1$ ，相频 $180°$ ），则在此处使得闭环传函远大于1，即剧烈震荡，也就是不稳定。

总结：低频段：定稳态误差；高频段：定对噪声的抑制度；中频段：稳定性、动态性能

幅角定理

设 $W(s)$ 在复平面一个封闭曲线内有 $P$ 个极点和 $Z$ 个零点（这个封闭曲线不能穿过极点或零点），若 $s$ 绕该封闭曲线顺时钟转一圈，则 $W(s)$ 绕原点顺时钟转 $Z-P$ 圈。

利用幅角定理说明Nyquist判据

令 $W=1+G_{open}$ ，再令 $s$ 转圈的轨迹为D形曲线，即（按：如果虚轴上有零极点，则应该绕过，后面进行说明）：

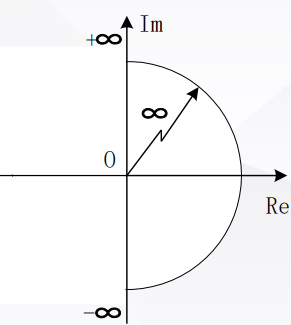
则 $s$ 转一圈， $W$ 就顺钟旋转了闭环极点数-开环极点数圈，而 $W$ 究竟顺钟转了几圈可以通过Nyquist图绕 $-1$ 点转的圈数定（因为 $s$ 为无穷时， $W$ 通常在原点蠕动，因此 $W$ 的轨迹就是Nyquist曲线），然后结合开环在D形曲线内的极点数即可解算出D形曲线中闭环极点数。若D形曲线内（即左半平面）闭环极点数非0，则系统不稳定，否则稳定。

当然，如果单纯是用来判断稳定性，则Nyquist判据恐怕还没Routh判据好用。但由此可以引出相对稳定性和裕度的问题。

问题：虚轴上有开环极点或闭环极点（即 $W$ 的零极点）时都需要绕开。例如绕开点 $j\omega$ 的方法是在此处代入 $j\omega+\epsilon e^{j\theta}$ ，（如果希望从正半平面绕过就）令 $\theta:-\frac{\pi}{2}\rightarrow \frac{\pi}{2},\epsilon\rightarrow 0$ ，然后把无穷小项抹掉即可看出幅角变化的范围，进而在Nyquist图中进行补完。

这是通用的方法，对非最小相位系统也适用。（非最小相位只用适时地把额外的180°相角加上去即可）

若上述 $\omega\neq 0$ ，则对应等幅震荡，其会在转折频率出发生相角突变（具体从多少跳到多少要带入计算）

延迟环节可能会形成螺旋线，（相比于惯性环节）延对系统稳定性不利。

相对稳定性（裕量）（重点）

比较相对稳定性时都讲的是稳定系统
有多种稳定性的度量方式，这里只考虑相角裕量和增益裕量。
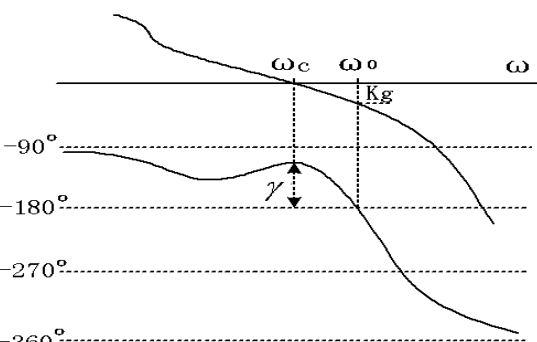
- 相角裕量 $\gamma=180°+\arg(G(j\omega_c))$ ，其中 $\omega_c$ 指剪切频率。
- 增益裕量 $K_g$ 是相角为 $-180°$ 时，幅频特性的倒数的分贝值（或幅频特性分贝值的相反数）。因此在bode图上的增益裕量为坐标值的负值。
稳定时，相角裕量、增益裕量为正。
二者有一定冲突，且也不是越大越好（过大则迟钝）；两个裕量都必须考虑。
以上只针对最小相位系统

考法：

Bode作图，或由Bode图反求传函

Nyquist简单作图判稳等

参数稳定性定性判断

开环频率特性定闭环特征

建议以-20dB/dec穿过时轴，且有一定中频带宽
相角裕量大，则超调小
剪切频率大，过渡过程时间小
典型四阶开环系统

回顾：高频段——抗干扰能力、响应开始阶段的状态，中频——稳定性、过渡过程时间，低频——静态误差。