第三章：控制系统的时域分析

介绍系统时域分析的办法。

前言

一般在时域只能分析一、二阶（这里的阶次指闭环传递函数分母多项式的阶数）的系统，对高阶系统可以尝试找找主导极点试图近似为二阶系统，如果做不到就彻底没辙了。

我们在评价系统状况时重点关注三个特征（“稳快准”）：

• “稳”：稳定性
• “快”：通常重点关注过渡过程时间
• “准”：静态误差（静差、稳态误差）

稳定性（”稳快准“的稳）

• 自治系统

即系统的微分方程组可以写成不显含时间变量的形式$\dot{X}=f(X)$。自治系统就是各个状态处的数学性质不随时间变化的系统，因此把初值放在任意时间点产生的解都一样（只相差一个时延）。

注意：自治系统不能等同于非时变系统。如果有时变的输入，则系统必然是非自治系统，但有可能是非时变系统。因为非时变系统其实是输入延迟后输出也有相同延迟的系统，因此其实其性质是和系统的内在性质有关，而和具体的输入信号是什么无关。

不过，自治系统一定是非时变系统。

• Ляпуно́в稳定性

设系统的状态变量矢量为$X$，系统可以写成微分方程组的形式$\dot{X}=f(X,t,u)$，其中$\dot{X}=\frac{\partial X}{\partial t}$，$u$代表输入变量，且该微分方程组满足解的唯一性定理。则Ляпуно́в稳定性表明可以通过控制初值的差异来限制此后演化过程中系统状态的差异。即：

若系统微分方程组在初始条件$X(t_0)=X_0$下有解$X(t)$，且$\forall \epsilon>0,\exist \delta>0$，使得初始条件改为任意满足$||\widetilde{X}_0-X_0||\le \delta$的$\widetilde{X}_0$后所得到的解$\widetilde{X}(t)$满足$\forall t>t_0,||\widetilde{X}(t)-X(t)||<\epsilon$，则称该系统的解$X(t)$是（Ляпуно́в）稳定的。

这本书（《自动控制原理》，吴麒等著）里的这个定义比通常使用平衡点的定义更一般。平衡点就是满足$\dot{X}=f(X,t,u)=0$的解。如果将上文的$X_0$指定为某个平衡点，则相应的解当然就是$X(t)\equiv X_0$。此时若这个解是稳定的，则称平衡点$X_0$是稳定的平衡点（常见的Ляпуно́в稳定性定义）。

对自治系统而言，由于从哪个时间开始考虑都一样，因此可以直接把定义中的$t_0$直接指定为$0$。

经典的示意图如下所示（图源未知，状态变量只有一个$x$）：

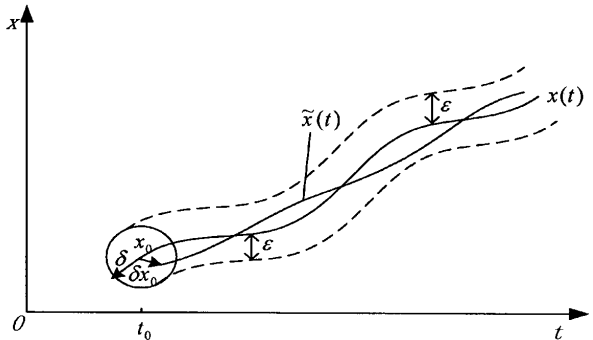
• 稳定范围

对Ляпуно́в稳定的解$X(t)$而言，通常给定的$\epsilon$越大，能容许的初始条件偏差$\delta$也可能会大一些。但有时即使$\epsilon\rightarrow+\infin$（即无论$\epsilon$取得多大），相应的$\delta$也总不能超过一个定常上确界$\delta_0$，则称$\delta_0$是该解处的稳定范围。（同理，若这个解就是某平衡点，则$\delta_0$是该平衡点的稳定范围）

• Ляпуно́в大范围稳定

对Ляпуно́в稳定的解$X(t)$而言，当其$\delta$（随着$\epsilon\rightarrow+\infin$）可以任意大（$\rightarrow+\infin$，或稳定范围不存在）时，则称这个解是大范围稳定的。（同理可定义大范围稳定的平衡点。）

• 渐进稳定

对Ляпуно́в稳定的解$X(t)$而言，若存在$\delta>0$，使得任意初值$\widetilde{X}_0,s.t.||X_0-\widetilde{X}_0||\le\delta$对应的解$\widetilde{X}(t)\rightarrow X(t)\space(t\rightarrow+\infin)$，则称称这个解是渐近稳定的。

注意：渐进稳定是比稳定更强的性质

• Ляпуно́в第一方法

不加证明地给出，当光滑系统局部线性化后，局部的传递函数极点：

1. 全在左半平面，则这个局部是渐近稳定的。
2. 有至少一个在右半平面，则这个局部是不稳定的。
3. 都不在右半平面，但有的在虚轴上，则无法通过线性化结果判定局部的稳定性。

• LTI系统的稳定性

由于LTI系统本来就是线性的，因此任意解的稳定情况都一样。因此只用讨论系统的稳定性。由于没有非线性项，因此只需要Ляпуно́в第一方法的前两条即可，第三条的临界稳定直接当成不稳定即可。

正因如此，非线性系统不能笼统地说整个系统是否稳定/不稳定，而只能说哪些状态（或哪些解）上稳定。

Routh判据

• 根据特征方程画Routh表。每行每个行列式的第一列两个数字是一样的，第二列数字顺次右移。行列式总是除以行列式左下元素的负值。

• 第一列只要不同号，就不稳定（考试只要求这个，以下只用参考即可）

  • 第一列从上向下顺次查看，变号几次就有几个根在右半平面
  • 如果第一列某个数算出来是0，则用一个小正数$\epsilon$代替，在后面可以约掉（如果约不掉，就按照“可以任意小的正数”来判断包含它的数的正负）。
  • 如果出现0且0前后变号，则对应一次变号；否则表示有一对纯虚根
  • 如果一整行都是0——解决：用其上一行作为辅助多项式，辅助多项式求导后的系数代替这个全0行
  • 其实还有很多种例外情况

• 上一章题型：框图化简+多输入算静差，etc

简化的判定方法

1. 如果系统稳定，则特征多项式所有系数必须全部大于0或全部小于0，（稳定的必要条件）

   注意：

   • 等于0也不行，即缺项就不稳定。
   • 注意：给特征多项式整体加个负号根不变，因此全部小于0也行。

2. 一、二阶上面的条件也是充要条件

3. 三阶除上面条件外再加一条就是充要条件：中间积大于两侧积。

参数稳定性

• 闭环特征方程=开环分子+分母（注意：通常给的是开环传递函数，但要考虑的是闭环是否稳定）

• 一般地，开环增益过大、时间常数增大/增多（这两个忽略高阶项时是一致的）不利于稳定。

  这几条判断的道理建议参考频率响应。

  时间常数增多，即有时$(T_1s+1)(T_2s+1)=T_1T_2s^2+(T_1+T_2)s+1\approx (T_1+T_2)s+1$，于是此时时间常数增多其实和时间常数变大基本一样。

• 解参数稳定性就是求闭环稳定时的参数范围。

静差（”稳快准“的准）

• 静差是只针对稳定系统的概念，就是指误差的终值。

  事实上，闭环系统的“误差”概念需要定义。以下无论是否为单位负反馈都认为误差就是指“输入信号减输出信号”。

  做题时，简便方法还是把输入、输出的稳态一算，输入稳态减输出稳态即可，不用真换成单位负反馈。

• 一般只考虑三种特殊输入信号下的静差

  • 单位阶跃$1,1/s$
  • 单位斜坡$t,1/s^2$
  • 加速度$0.5t^2,1/s^3$

  注意：加速度信号的时域表达式有个1/2的系数，其他的特殊输入信号系数为1。

• 然后有对应的误差系数和稳态误差公式（算误差系数时不用管输入了，因为在其定义中已经考虑了；同时误差系数用的是单位负反馈的开环传递函数）（图源课程ppt）

• 误差系数增大，有利于减小静差。因此在稳定的前提下增大开环增益有利于减小静差。同时提高系统型次（指开环积分器数量）也能减小静差。这就是改善系统静差的两个主要方案。

课件pp36的框图的原理：

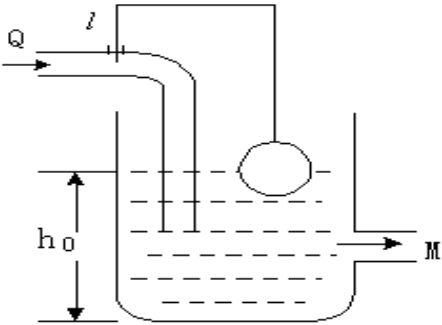
$Q$，$M$为流量，$(Q-M)dt=kdh\rightarrow (Q-M)=ksH$

$h$又通过伯努利方程决定流出量$M$，则可以算出来$M=\alpha h$

加电机时误差和电流以及转速成正比，因此到阀门开度以及流入量就出现一个积分环节（电动机可以假设为一阶模型）

扰动静差

利用线性系统的叠加原理！分别看只有输入（上面已经讨论）和只有扰动（其实在下述特殊结论不可行时只能硬算）的静差，然后加起来即可。

• 引入扰动点前有积分环节，则对阶跃扰动无静差（输入到阶跃的传递函数为0）；否侧阶跃扰动静差非0

注：pptp40的省略的分母因子是$Ts+1$的形式

有时可以通过等效为扰动来简化静差的计算。

动态指标（”稳快准“的快）

• 上升时间、延迟时间、峰值时间等（这些不重要）

• 过渡过程时间（稳态时间）

• 超调量（注意是比例）

二阶公式

• 特征方程$T^2s^2+2T\xi s+1=0$

• 自振角频率$\omega_n=\frac{1}{T}$、阻尼振荡角频率$\omega_d=\frac{\sqrt{1-\xi^2}}{T}$

• 一对共轭虚根时，极点为$-\omega_n\xi\pm j\omega_d$。进而得到二阶欠阻尼系统极点的几何含义：

  • 到原点的距离是$1/T$
  • 和负半轴夹角的余弦是$\xi$（和超调反相关）（夹角$\theta$本身和超调正相关$\exp (-\pi/\tan\theta)$）
  • 实部绝对值（到虚轴距离）是$\xi/T$（和过渡时间反比例相关）
  • 虚部绝对值（到实轴距离）是$\omega_d$（和峰值时间反比例相关）

• 超调公式 $\sigma=\exp(-\pi\xi/\sqrt{1-\xi^2})$

  超调和时间常数无关。

• 过渡过程时间估计公式 $t_s=3T/\xi$（5%）或$t_s=4T/\xi$（2%）

  注：$t_r$公式的θ见前二页ppt

• 峰值时间公式 $t_p = \pi /\omega_d$

高阶近似

看的是闭环传递函数

根据留数大小和衰减速度确定是否可略去。剩下的极点是主导极点

• 若某极点（或一对共轭极点）远离（实部是3~5倍以上）原点和其他零极点，则可略去
• 若某极点和零点很近（构成偶极子），则对应极点的模态占比小，可以同时近似地零极点相消。

注意：去掉无关的极点时要保证闭环静态增益相同（可能要改k）。

校正

串联校正

• 比例控制器：比例变大，时间常数和阻尼系数都变小——响应快，过渡时间不变，超调变大，减小稳态误差（如果非0）
• 积分控制：减静差，系统变慢，可能不稳定（PI，滞后校正）
• 考虑超调：分析曲线可知应该把微分引进来减小超调（PD，超前校正）
• 综合：PID

注意：PID是并联

局部反馈校正

（可忽略）