ANCSH简介

NOCS的超级加强版，可以针对一整类的铰接物体（articulated objects）估计各部分的尺寸和位姿（当然对变形有一些限制）。

原论文：https://arxiv.org/abs/1912.11913

ANCSH（Articulation-aware Normalized Coordinate Space Hierarchy）是对NOCS的自然扩展，将其推广到铰接物体的位姿估计上。

铰接物体就是可以将其分成多个刚体（称为部件（parts）），且一些部件之间有一些铰链（joint）“相连”，使得被连接的部件可以相对地做（通常会有约束的）刚体运动。

示例：游标卡尺可以当成游标和尺两个部件；微波炉可以分为门和炉体两个部件，且二者之间的铰链有门轴的约束。流体、柔软的物体严格而言不是铰接物体。

在这篇工作中，作者只考虑两种特殊形式的铰链：

旋转铰链（revolute joints）

平动铰链（prismatic joints）

同时作者假设同类的铰接物体应该有着相同的部件和相同种类的铰链。

这篇工作希望训练一个模型，在显式给出一些关于给定类别的结构信息（如指明微波炉这类铰接物体只有两个部件，二者之间为旋转铰链）后，就能对一个类别的铰接物体（例如：任意形状、开闭状态的各种微波炉）的各个部件实现位姿和尺寸估计（category level）。

当然，ANCSH和NOCS一样，不要求显式地给出canonical frame中的点云信息。和canonical frame类似地，为了铰链的运动状态有所参照，则总是假设ANSCH中各个关节都存在一种静息态（rest state，例如假设微波炉门轴的静息态就是关上的），于是铰链状态就是相对静息态的状态。

类别的结构信息不影响整体框架，只是最后的输出维数略有区别。

其实可以考虑放松这个要求，让模型通过类似RNN式的方法自行找出部件（这类文章已经有114514篇，略）

形式化定义（符号表）

输入

（世界坐标系下的）某物体的点云 $P=\{p_i\in\mathbb{R}|i=1,...,N\}$
- 这个点云可以是从单张RGBD图像lift得到的（具体细节参考NOCS，这里假设已经有了点云），因此完全可以处于任意位姿，也可以因遮盖等不全。
- 该点云对应的物体应该是某个已知的铰接物体类中的一个（可以是未知的）实例（如：微波炉中的某一特定形状的微波炉）。
该类物体一共有 $M$ 个部件（parts），记为 $\{S^{(j)}|j=1,...,M\}$
- 这里的 $S^{(j)}$ 只是记号，并不是说需要输入每个部件的点云等三维模型；实现时我们只需要确定有 $M$ 个部件即可。
该类物体一共有 $K$ 个类型已知的铰链（joints），记为 $\{J_k|k=1,...,K\}$
- 这里的 $J_k$ 和上面的 $S^{(j)}$ 是一个道理。铰链的类型没有通过数学符号显式地写出，但对每个 $J_k$ ，其是旋转铰链还是平动铰链都是已知的（作者只考虑这两种铰链）。
- 铰链的类型完全不影响网络模型的结构，只影响我们对网络输出的识读方式和后续处理（见后）。

输出

对输入点云按照部件的一个分割 $\{S^{(j)}|j=1,...,M\}$ （这里的 $S^{(j)}$ 就确实指第 $j$ 个（这个序数是人为指定的）部件的点云）
每个部件的旋转矩阵 $\{R^{(j)}\}$ 、位移 $\{t^{(j)}\}$ 、尺寸 $\{s^{(j)}\}$ （注意大小写）。
每个铰链的参数 $\{\phi_k\}$ ${ϕ_{k}}$ 和状态 $\{\theta_k\}$ ${θ_{k}}$ （不同种类的铰链有不同的参数和状态定义）
- 对旋转铰链，参数是转轴矢量 $u_k^{(r)}$ (r:rotation)和转轴上的一点（pivot） $q_k$ ，状态是相对静息态的转角。
- 对平动铰链，参数是平动方向矢量 $u_k^{(t)}$ (t:translation)，状态就是相对静息态平动的距离。

ANCSH

为了给每个部件估计位姿和尺寸，我们应该给每个部件都隐式地确定一个NOCS；为了确定各个铰链的静息状态，我们也应该给整个铰接物体隐式确定一个NOCS。这就是本文的核心——给物体整体和各个部件都分别确定一个NOCS，形成了层次结构（Hierarchy）。

第零层：Normalized Articulated Object Coordinate Space (NAOCS)
- 每个铰链的静息状态 $\theta_{k0}$ 就在NAOCS中确定
第一层：Normalized Part Coordinate Spaces (NPCSs)
- 当然，每个部件的指向也是在NAOCS中确定，NPCS中部件指向应该和NAOCS中的相同。即从NPCS到NAOCS中的对应部件只需要经过尺度和平移变换。
- 造NPCS层还有一个好处：不同类别物体可能有相同的部件，这样就为类别间的泛化提供了可能（当然这篇文章没做这件事）。

按：其实从某种意义上还可以往上垒，考虑一些part工作中的与或树结构。

最终用了两个不同的网络来回归NAOCS和NPCS。（图源原论文）

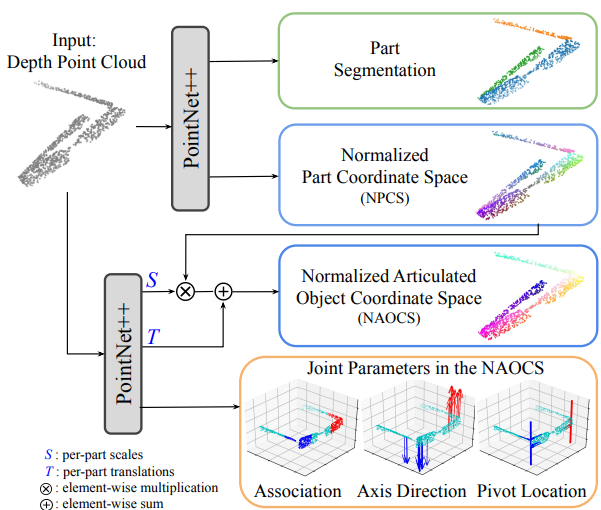
part segmentation head

就是输入整个物体点云，输出逐点的（ $M$ 维）属于各部件的概率（注意 $M$ 是已知的）。这就是一个分类问题。

NPCS head

输入整个物体点云，输出逐点逐类别的NPCS坐标，再用上面partition的结果把正确的NPCS坐标提取出来。（同样，这里还是可以避免类间竞争，参见NOCS和maskRCNN中最后部分的实现）

以上两个head输入量相同，因此共用相同的pointnet++的backbone抽取特征是合理（且经济）的。

NAOCS head

输入还是整个物体的点云，为NPCS中的每个点预测其（从NPCS）到NAOCS的变换 $\{G^{(j)}_i=(G_{t,i}^{(j)},G_{s,i}^{(j)})|j=1,...,M,i=1,...,N\}$ ，其中 $G^{(j)}_{t,i}$ 和 $G^{(j)}_{s,i}$ 分别指第 $i$ 个点 $p_i$ （当假设 $p_i\in S^{(j)}$ 时）变换到NAOCS的平移量和尺度缩放量。

这里还是和前面一样，先把每个类的平移量和缩放量都预测出来，然后再用segmentation的结果取出正确的平移量和尺缩量。

设 $p_i\in S^{(j)}$ ，其在NPCS中的对应点为 $c_i$ ，在NAOCS中的对应点为 $g_i$ ，则有：

$g_i=G_{s,i}^{(j)}c_i+G_{t,i}^{(j)}$

最后，每个部件总体的 $G_t^{(j)},G_s^{(j)}$ 由属于该部件的 $G^{(j)}_{t,i}$ 和 $G^{(j)}_{s,i}$ 求平均而得。

注意：之前已经假设过NPCS和NAOCS中各个部件的指向一样，因此没有旋转，只有平移和缩放。

joint head

输入物体整体点云，输出在NAOCS中的铰链参数（对旋转铰链，参数为转轴方向向量和转轴上一点；对平动铰链，参数为移动的方向矢量）。

这里没要求预测铰链状态。

这里要求预测的参数指的是在NAOCS中的参数，后面还需要通过位姿估计量将其转化到世界坐标系。例如NAOCS中转轴的指向一般和世界坐标系中的转轴指向不相同。这篇文章中用打 $'$ 点的符号代表NAOCS中的参数。

达到这个目标，首先需要对每个铰链确定哪些点和该铰链相关联（associate），即确定 $\{a_i|a_i\in \{0,...,K\},i=1,...,N\}$ （ $a_i=0$ 表示未与任何铰链相关联）。关联的ground truth使用以下方法生成：

旋转铰链：距转轴距离在 $\sigma$ 内的点与该铰链关联；
平动铰链：两个部件中“移动”的那个部件上所有点都和该铰链关联；

有无可能有一个点同时关联到多个铰链？对旋转铰链，只要控制 $\sigma$ 足够小就能保证没有公共覆盖的部分。对平动铰链，“移动”部件的定义需要由类的信息直接给出（如规定柜子的抽屉是移动部件，而柜子的柜体不是）。虽然这个概念可能没法直接推广到各种物体上，但确实使得平动铰链不会产生覆盖。

随后在每个点上回归出一个7维向量，最后用和各个铰链相关的所有点vote出每个铰链的参数（再次提醒：不包括铰链的状态）。

这个七维向量的含义是这样的（前面已经提到，每个铰链的类型是预先给定的已知量）：

对平动铰链，前三维（单位化后）是NAOCS中的平动方向 $u^{(t)'}$ ，剩下的四维就丢弃掉。
对旋转铰链，前三维（单位化后）是NAOCS中的转轴方向 $u^{(r)'}$ ，接下来三维（单位化后）代表NAOCS中从这个点出发指向转轴且和转轴正交的方向矢量，最后一维代表NAOCS中这个点到转轴的距离。

为什么不直接预测到转轴上一点的方向矢量？因为“转轴上一点”不是唯一的，因此用上述这种有些奇怪的方法更好。

最后把关联的点的参数“平均”或者voting一下即可得到铰链的参数。

由于NAOCS head和joint head的目标空间都是NAOCS，因此二者可以共享一个pointnet++的backbone。

Loss

segmentation loss: relaxed IoU loss (类似IoU，但是可以计算两个mask之间的IoU，参考https://arxiv.org/pdf/1809.07417.pdf)
association loss: relaxed IoU loss
NPCS，NAOCS都用点上的均方误差。
关节参数用均方误差。

最后把这五个损失项做个线性组合得到总损失。

Kinematic Constrains

在NOCS中，直接使用梅山方法即可获得位姿和尺寸的估计量。在ANCSH中当然也能如此估计，但是这就忽视了铰链对各个部件的位置约束。这不仅会导致位姿估计不正确，还可能严重影响最后的铰链状态估计。因此需要把铰链带来的运动约束考虑进去。

我们在上面的网络模型输出中可以得到：

部件的分割（part segmentation）
各点 $p_i$ 在NOCS中的对应点 $c_i$
各个部件 $S^{(j)}$ 从NOCS映射到NAOCS的平动 $G_t^{(j)}$ 和尺度缩放 $G_s^{(j)}$
各个铰链 $J_k$ 在NAOCS中的参数 $\phi_k'$

利用这些量，我们希望输出：

每个部件 $S^{(j)}$ 在世界坐标系中的位姿和尺度 $R^{(j)},t^{(j)},s^{(j)}$

因此优化步骤为：

先用梅山算法搞出一个初始位姿和尺度；
再固定尺度估计量 $s^{(j)}$ ，考虑关于铰链的运动约束的损失对旋转矩阵和位移向量做非线性最小二乘法。

上面第二步的损失=梅山算法中的二范数损失+各个铰链上的损失之和。

铰链的损失和铰链的类型有关（设由当前铰链的连接的两个部件分别为 $S^{(j_1)},S^{(j_2)}$ ）：

旋转铰链的损失是简单的二范数

$e_k=||R^{(j_1)}u_k^{(r)'}-R^{(j_2)}u_k^{(r)'}||$

将NAOCS中的转轴方向矢量 $u_k^{(r)'}$ （前面已经说明，这个方向矢量和NPCS中转轴的方向矢量完全一致）乘上旋转矩阵就是世界坐标系中的转轴方向矢量 $u_k^{(r)}$ 的一个估计。

我们要求该铰链连接的两个部件的旋转矩阵能把转轴映射到相同的方向，这就使估计的旋转矩阵更加合理。
平动铰链的损失由两部分构成：
- 两个部件旋转矩阵应该尽量相同，即损失定为（注意旋转矩阵是正交阵）
  
  $||R^{(j_1)}R^{(j_2)T}-I||^2$
- 两个部件的相对位移向量应该和平移向量平行。这一步论文没有细说，将结合自绘图说明（按：把中心点移到了原点，其实效果基本是一样的）：
  
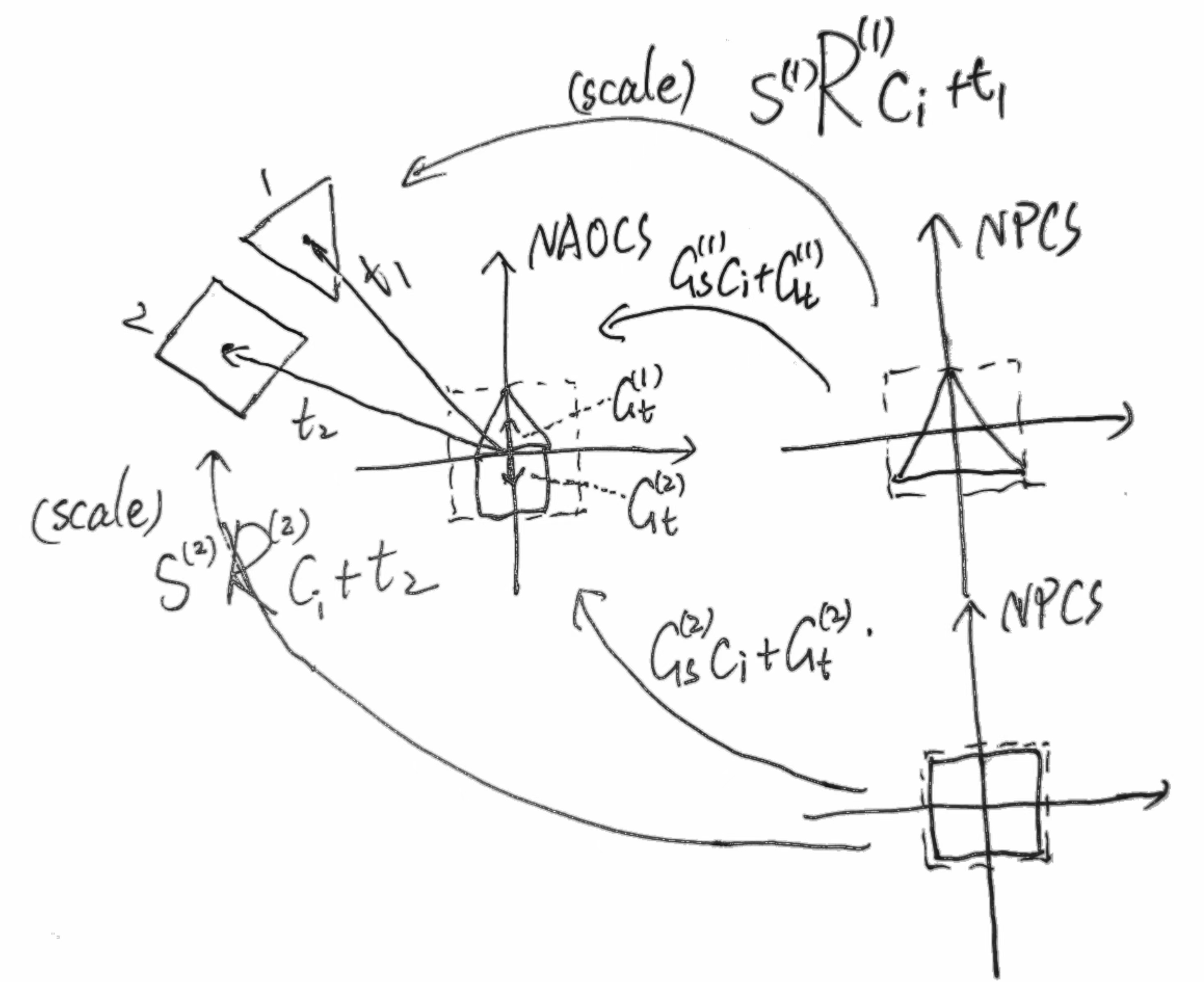
  某有两个部件，一个平动铰链的二维物体的计算过程如上图所示。由于完整的铰链物体几乎总是比单个物体大，因此我们通常有 $G_s^{(j)}<1$ 。于是由上图直观得到真正的位移向量（方向代表位移方向，模代表位移长度）其实是:
  
  $t_2-t_1+\frac{s^{(1)}R^{(1)}}{G_s^{(1)}}G_t^{(1)}-\frac{s^{(2)}R^{(2)}}{G_s^{(2)}}G_t^{(2)}$
  
  但作者在损失中使用的是：
  
  $\delta_{1,2}=t_2-t_1+\frac{s^{(1)}R^{(1)}}{1}G_t^{(1)}-\frac{s^{(2)}R^{(2)}}{1}G_t^{(2)}$
  
  使用这个量的原因不明。但是作者在代码中的（优化这部分的）损失和他论文里写的损失完全不一样。
  
  我们期待自然坐标系中的铰链参数（位移单位方向向量 $R^{(j)}u_k^{(t)'}$ ）应该和上面推算的位移向量共线，因此有损失项：
  
  $\sum_{j=1,2}||R^{(j)}u_k^{(t)'}\times \delta_{1,2}||^2$
  
  当然，这里的外积可以用李代数的方法改为矩阵乘积（具体方法参考讲rotation的blog或自行google）

以上的损失按一定系数线性组合就得到总损失项。

Joint Param & State in Camera Space

有了每个部件的 $\{R^{(j)},t^{(j)},s^{(j)},G_t^{(j)},G_s^{(j)}\}$ 后，即可对世界坐标系中的铰链参数和铰链状态进行估计。

对旋转铰链， $R^{(j_1)}u_k^{(r)'}$ 和 $R^{(j_2)}u_k^{(r)'}$ 都是对世界坐标系中转轴方向的合理估计，因此最终转轴方向就是二者求平均再单位化。转轴上的一点用 $t^{(j_1)}+\frac{R^{(j_1)}s^{(j_1)}}{G_s^{(j_1)}}(q_k'-G_t^{(j_1)})$ 或 $t^{(j_2)}+\frac{R^{(j_2)}s^{(j_2)}}{G_s^{(j_2)}}(q_k'-G_t^{(j_2)})$ 均可（其中 $q_k'$ 是该旋转铰链在NAOCS中的转轴上一点，这些公式可以参考上面的手绘图很容易地得出），因此最终这个点就是两种估计的平均。由于旋转铰链相连两部件的转动共轴，因此可以直接用角轴式中算转动角差的公式（参考rotation的blog或google）计算其状态。

对平动铰链，平动方向估计类同转轴方向估计，状态（平动距离）就是 $||\delta_{1,2}||$ （如果作者的计算是正确的话）。