最优位姿估计中的梅山（Umeyama）算法

介绍在已知刚体运动+尺度变换前后模型的对应点后，如何得到最优的刚体运动（和尺度变换）估计。

Pose

要谈论刚体运动或尺度变换，则必然是在讨论同一物体两个坐标系（frame）之间的运动/尺度关系。如果只是给出一个物体的单个三维模型，是没有办法定义其运动或位姿的。

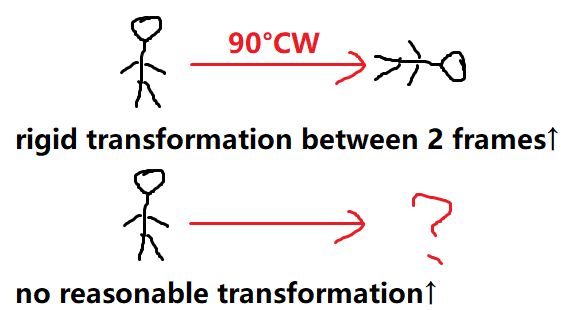
因此，谈论物体位姿（pose）时，我们都必须先假想存在一个“正规的坐标系”（canonical frame），然后再以该物体当前坐标系到正规坐标系的刚体运动和尺度变换为其位姿或尺度。

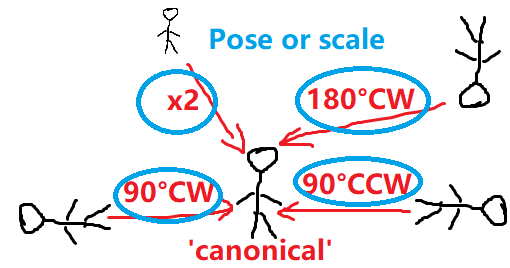
正规坐标系可以是显式（以正规坐标系下的点云的形式）提供，也可以（通过提供此物品运动后的点云+刚体运动参数和尺度参数等）隐性地给出。

Umeyama Method

现在我们需要估计在两个坐标系中的同一物体之间的刚体运动和尺度变化。假设我们用两个点云分别表示两个坐标系中物体，已知这两个点云在同一公共坐标系中的坐标和两个点云之间点与点的对应关系（匹配）时，可以用梅山（Umeyama）方法估计刚体运动和尺度（进而可用于估计位姿）。

注意：没有点与点的对应关系时没法直接使用梅山方法。

设$P'=[p_1,...,p_n]_{3\times n},Q'=[q_1,...,q_n]_{3\times n}$就是这两个点云，且$p_i$与$q_i$相匹配，则记由$P$到$Q$的旋转、位移和尺度放缩为$R\in M^{3\times 3},t\in \mathbb{R}^3,s\in\mathbb{R}$。若点云数据完全精确，则有：$\forall i,sRp_i+t=q_i$

注意：这里旋转、位移和尺度放缩的施加顺序对估计结果是有影响的。上式只是展示了一种施加方式。

若点云数据不精确时，即可通过解如下优化问题获得一个最优估计：

$\min_{s,R,t} J= \sum_i ||sRp_i+t-q_i||_2^2$

$s.t. R^T=R^{-1}$

首先估计$t$。记$\bar{p}=\sum_ip_i/n,\bar{q}=\sum_iq_i/n$，则

$J=\sum_i||((q_i-\bar{q})-sR(p_i-\bar{p}))+(\bar{q}-sR\bar{p}-t)||_2^2$

$=\sum_i||(q_i-\bar{q})-sR(p_i-\bar{p})||_2^2+||(\bar{q}-sR\bar{p}-t)||_2^2+2((q_i-\bar{q})-sR(p_i-\bar{p}))^T(\bar{q}-sR\bar{p}-t)$

$=\sum_i||(q_i-\bar{q})-sR(p_i-\bar{p})||_2^2+||(\bar{q}-sR\bar{p}-t)||_2^2$

因此$t$的最优值就是$\bar{q}-sR\bar{p}$。

设$P=[p_1-\bar{p},...,p_n-\bar{p}]_{3\times n},Q=[q_1-\bar{q},...,q_n-\bar{q}]_{3\times n}$，则优化问题可以写成

$\min_{s,R}J=||Q-sRP||^2_{F}$

$s.t.R^T=R^{-1}$

这里的$||\cdot||_F$指Frobenius范数，即把矩阵所有元素平方求和再开方。因此这里的损失函数和前面是一样的。其严格的数学形式为$||M||_F=\sqrt{tr(M^TM)}$

于是有：

$J=tr((Q-sRP)^T(Q-sRP))$

$=tr(Q^TQ)-tr(sP^TR^TQ)-tr(sQ^TRP)+tr(s^2P^TR^TRP)$

$=tr(Q^TQ)-2ns\cdot tr(P^TR^TQ)+ns^2\cdot tr(P^TP)$

等价于最小化：

$J'=-2s\cdot tr(P^TR^TQ)+s^2\cdot tr(P^TP)$

当$R$取定时，最小化要求$s=\frac{tr(P^TR^TQ)}{tr(P^TP)}$（*）

将其代回$J'$有：

$J'=-\frac{tr(P^TR^TQ)^2}{tr(P^TP)}$

因此等价于最大化$J''=tr(P^TR^TQ)=tr(R^TQP^T)$

到此为止此问题与正交普鲁克问题（Orthogonal Procrustes Problem，即$s$恒为1的梅山问题）等价。此时的点云配准算法又称Kabsch算法。

对$QP^T$进行SVD分解，则：

$J''=tr(R^TUDV^T)=tr(V^TR^TUD)$

其中$D$为对角阵（由于都是三维点，因此$QP^T$是方阵；注意奇异值都是非负的），$V,U$为正交阵。注意到$V^TR^TU$整体也是一个正交阵，因此每列的模是1；而$D$的作用只是给$V^TR^TU$每列对应乘一个非负的数。因此，想让$J''$最大，应该把$V^TR^TU$各列的方向扭到对求迹最有贡献的地方，因此得到$V^TR^TU=I$。

于是$R=UV^T$，$s$可以通过代回（*）式求出。

提示：到此为止梅山问题即告解决。但是需要注意三个问题：

1. 用来做位姿估计的两个点云必须有点与点之间的匹配关系。如果没有这个信息则此算法无用武之处。
2. 算法对点数$n$没有上限。但为了避免离群点对估计结果的影响，建议尝试RANSAC等更合适的方法。
3. 但是点数太少也不正确。在点数少于3或点数为3且三点共线时，方程$J=0$是欠定的。