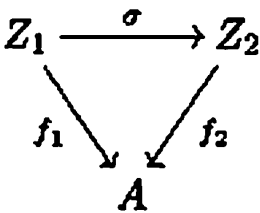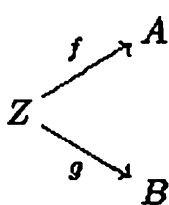介绍范畴相关内容,包含原书第一章第3节内容。增补了关于NBG公理体系的内容。部分内容和名词翻译参考了https://zhuanlan.zhihu.com/p/364284965系列专栏。
abstract nonsense: 抽象废话,特指范畴论的语言。因为它只关注“结构”,而非关注“含义”,即具体的集合元素。
NBG Set Theory
von Neumann–Bernays–Gödel集合论公理体系是ZFC公理体系的一个保守拓展(conservative extension)。NBG体系的一个特点是可以区分类(class)和集合(set)。类的概念比集合更为广泛,例如可以定义“所有集合所组成的类”。(根据正则公理,ZFC公理系统中不存在“所有集合所组成的集合”)。
事实上,保守拓展就是说:NBG可以谈论比集合更宽广的概念“类”,且关于集合的陈述在NBG中可证明当且仅当其在ZFC中可证明。
NBG的原始对象是类、一个表示“是集合”的谓词R和成员关系∈。
R的定义是:类x是集合(即R(x))当且仅当存在一个类X,使得x∈X。不是集合的类称为真类(proper class)
(这种定义下)∈可以用在类与类之间。
注:这里有两种定义途径,以上显示的是Godel的叙述方法。另一种Bernays叙述方法则∈左侧只能是集合,但可以通过表示(representation)概念“圆”回去。
Category
以下注意区别用来表示范畴的正体C和表示对象等的斜体C
一个范畴C由以下两份东西构成:
-
一个包含了C所有对象的类(记为Obj(C))
-
C中任意两个对象A,B,都存在一个态射(morphism)的类HomC(A,B)满足以下性质(结合律、幺元律):
-
对C中的任意对象A,都至少存在一个“恒同”(identity)态射1A∈HomC(A,A)
-
态射可以“复合”(composition),即两个如下形式的态射f∈HomC(A,B),g∈HomC(B,C)可以决定一个新态射gf∈HomC(A,C)。等价地说,即任意三个对象A,B,C,都存在一个函数:
HomC(A,B)×HomC(B,C)→HomC(A,C)
(f,g)↦gf
-
"复合"可结合。(fg)h=f(gh)
-
"恒同"映射的特点体现在”复合“中。即f∈HomC(A,B),则f1A=1Bf=f
-
除非A=C,B=D,否则HomC(A,B)∩HomC(C,D)=∅
可以形象化地把Hom想成函数集。
另外,在范畴C已经明确后,可以把f∈HomC(A,B)简写为f:A→B。由此即可画图(diagram)。
示例:集合和集合上定义的函数可以构成一个范畴。这个重要的范畴没有统一的记法,通常写成Set的某种花体(以下写成SET)。
示例2:设S为集合,∼是S上满足自反性和传递性的一个关系,则可以定义:
-
”对象“为S的元素;
-
”态射“集Hom(a,b)=(a,b)若a∼b,否则Hom(a,b)=∅
-
态射的合成就定义为∼的传递性:(a,b)(b,c)=(a,c)。
用这对”对象“和”态射“也可以构造出一个范畴。
特别地,∼可以取为=,≤,⊂等等。这种范畴总是可交换的(概念见下,这是因为这种范畴的态射只和”起点“和”终点“有关),在代数几何之类的地方很有用。
endomorphism
自同态即形同HomC(A,A)(记为EndC(A))的态射集中的态射。
根据对范畴的定义有1A∈EndC(A)。同时,f,g∈EndC(A)则fg∈EndC(A)。
commutative diagram
若图上任意两个对象间的任意路径的合成都相等,则这个图是可交换的。
discrete
当所有态射都是恒同态射时,称该范畴离散。
上述”示例2“中∼取”=“时就可以得到离散范畴。
slice category
切片范畴特指一种由范畴构造范畴的方法。
设C是范畴,A∈Obj(C),则将新范畴CA定义如下:
有的地方将切片范畴CA记成C/A,而将共切片范畴CA(见后)记成A/C。
-
Obj(CA)就是所有(从Obj(C)中任意元素)指向A的态射的集合。
-
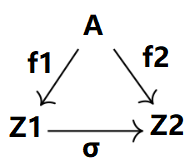
对任意f1,f2∈Obj(CA),若存在C的一个态射σ使得f1=f2σ,则称含有σ,f1,f2的子图是CA中的f1→f2的态射。参考下图(图源原书pp23):
注意:这里的要求不只是态射σ存在,还要求f1=f2σ,也就是说下图是可交换图时,这个子图才是CA的一个态射!
-
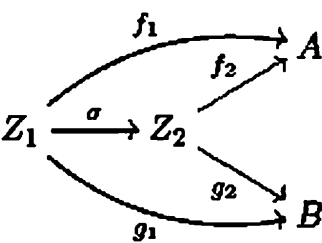
CA态射的复合,就是C中对应态射的复合所得到的子图。参考下图(pp23):
可以验证,这样定义的切片范畴CA满足范畴的定义。事实上,切片范畴是逗号范畴(comma category,谁起的鬼名字……)(逗号范畴还没定义)的一种。
当然,这个概念还可以进行拓展,例如我们可以定义两个元素构造出的切片范畴。设A,B∈Obj(C),则切片范畴CA,B可以定义为:
-
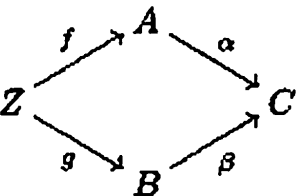
Obj(CA,B)的元素就是(从Obj(C)的同一元素出发)分别到达A和B的一对映射(f,g)所组成的图,见下(pp25):
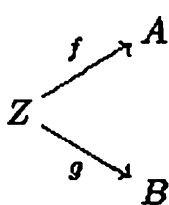
-
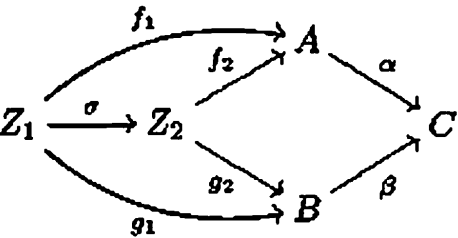
(f1,g1)→(f2,g2)的态射的定义:若存在函数σ同时满足f1=f2σ和g1=g2σ,则称σ,f1,g1,f2,g2组成的可交换子图是态射,即下图应当是可交换子图(pp25):
当然,我们还可以拓展到两个同终点的态射构造出的切片范畴。
设我们在范畴C选定两个这样的态射α:A→C,β:B→C。则新范畴Cα,β定义为:
-
Obj(Cα,β)的元素是(从Obj(C)的同一元素出发)分别到达A和B的一对映射(f,g)和α,β构成的子图,且是可交换子图(即αf=βg),见下(pp25):
-
态射是和σ相关联的如下图,且该图可交换(pp26):
coslice category
共切片范畴可以看成切片范畴的一种”对偶“。切片范畴定义里面所有箭头反过来,就是共切片范畴的定义。具体而言,就是说:
-
Obj(CA)就是所有从A出发的态射(指向Obj(C)中任意元素)的集合。
-
对任意f1,f2∈Obj(CA),若存在C的一个态射σ使得σf1=f2,则称含有σ,f1,f2的可交换子图是CA中的f1→f2的态射。参见下图:
仿照前面的说法,我们同样可以定义两个元素构造的共切片范畴,两个同终点的态射构造出的共切片范畴等。
pointed set (category)
令C=SET,A={∗}(即某个固定的单元素集),则有点集范畴(记为SET∗)定义为共切片范畴A/C={∗}/SET。
有点集范畴的对象就是函数f:{∗}→S(注意SET的态射就是集合上定义的函数),其中S是集合。因此f(∗)∈S,即有点集范畴的每个对象可以从每个集合中选择一个元素。因此,对象f:{∗}→S也可以用一个二元组等价地表示为(S,s),其中S是f的值域,s=f(∗)∈S。
因此,有点集范畴的态射(S,s)→(T,t)(可以等价地)指某个集合上的函数σ:S→T,且σ(s)=t。
有点集范畴的对象集Obj({∗}/SET)中的各个对象(形同(S,s))就是有点集(pointed set,或based set,rooted set)。
有点集和普通集合的区别在于,每个有点集都存在一个被选出的、特殊的、可辨的特殊元。例如,这个特殊元在群论中就是指单位元。
subcategory
C的子范畴C′定义为:
- Obj(C′)是Obj(C)的子类。
- ∀A,B∈Obj(C′),HomC′(A,B)是HomC(A,B)的子类。
- C′恒同态射、态射的复合和C相同。
子范畴是满的(full),若上述第二条改为HomC′(A,B)=HomC(A,B)。
和图论的子图,导出子图可以类比。
subobject classifier
有时可以像讨论集合的子集一样讨论对象(未必是集合)的子对象(subobject)。对范畴C和其中一个对象A而言,A的子对象和态射A→Ω之间一一对应,其中Ω是C的一个固定的对象。这个Ω就是子对象分类器。
对范畴SET而言,Ω={0,1}就是一个子对象分类器,此时子对象就是子集。