PSTNet简介

简单介绍PST（point spatio-temporal）卷积的原理，掺杂大量个人浅见。

论文：https://arxiv.org/pdf/2205.13713.pdf

Task

PSTNet希望解决的是点云时间序列的特征提取问题，从而有利于下游任务（语义标注、分类、etc.）的进行。

过去用过的方法：

栅格化（Voxelize），然后按照（类似一般视频的方式）造出四维卷积核提取特征。（例：Minkowski CNN）

问题：计算量大，栅格化过程有量化误差。

把时间维附加在各点的三维坐标上，即每个点的坐标为四维，然后用Pointnet++之类方法做静态的点云处理。（例：MeteorNet）

问题：丢失了时序信息，时间维的数量级和空间维通常不可比较等等。

PST Conv

基于点云序列在时间（规则间隔、有序的“帧”）和空间（无序点集）的不同特点，作者认为应该把时间维的卷积和空间维的卷积解耦。先在空间维度进行卷积，然后再在时间维度进行卷积。

spatial conv

注意和稀疏卷积（Sparse Conv）相区别。

考虑静态点云（单帧点云/普通点云）的卷积方法。由于点云不像二维图像像素或三维体素（Voxel）那样地规则分布，因此没法直接使用规则的、离散的卷积核。点云的点可以分布在空间中的任何位置，因此应当将点视为连续的变量，使用连续的（即在空间中处处有权重，而非只在特定格点上有权重）卷积核对每个局部进行处理。

理论上，卷积核可以选为高斯核（但可学习参数太少）、线性核（一个线性函数，计算量小，和普通卷积最接近）、插值得到的核（用离散核插值得到）等等，甚至（广义地）可以使用网络结构处理局部的特征。这篇文章中，作者使用了线性核（在表征能力和计算量、训练难度上达到了平衡）。

这篇文章的核函数形式为 $f_{\theta}:\mathbb{R}^{1\times 3}\rightarrow \mathbb{R}^{C_m\times C}$ ，其输入为平移后的点坐标（见后），输出为将上一层的 $C$ 维特征向量转化为 $C_m$ 维中间特征向量（指之后还会在时间维上卷积）的核，具体表达式为 $f_{\theta}(x)=\theta_d x\cdot 1\odot\theta_s$ 。其解释是 $\theta=[\theta_d,\theta_s]$ ， $\theta_d\in\mathbb{R}^{C_m\times 3}$ 是真正和平移后点坐标相关的线性函数， $\theta_s\in\mathbb{R}^{C_m\times C}$ 是和点坐标无关的、所有点共享的一个线性函数， $\odot$ 表示逐元素相乘。（按：其实拥有完全自由度的线性函数应该是一个三维张量，这里的形式其实是在 $C$ 所在维度上进行复制，消去了一个自由度，大大减少参数数量。但为何如此消去原因未知）

如果我们只希望卷积核反映局部的特征，则应该保证核函数在距离原点较远的位置有极小（或0）的值。这通常是通过选择点云中的点（而非改造核函数）达成的。

首先，我们通过某种方法获得点云的一个子集（称为“锚点”（Anchor））。文中使用FPS（可以参考往期blog）完成这一步。这一步也控制着点云序列在空间的降采样速率。
然后用KNN或“某个距离内的邻近点”为各个锚点确定“局部”。文章使用了“某个距离内的邻近点”方法。PointNet++论文在面临相似任务时，认为用距离选邻近点优于KNN，因为这可以保证特征所对应的尺度不变。
最后使用由局域中的点确定的各点处的权重，对各点的特征向量进行卷积（因此和普通卷积不同，PST必须把锚点坐标显式地传给下一层）。注意到“把卷积核移动到每个锚点对应的邻域中”和“把局部的点平移，使得锚点坐标为0”是等效的，因此实际中多使用后者，即局域中的点需要减掉锚点的坐标（这是本文的方法，有的文章则进行的是零中心化，这对结果的影响未知）

对于动态点云，我们只用在当前帧（时域锚定帧）中选中的锚点，并把他们向前后数帧（由时间核的长度确定）传递作为前后数帧的锚点即可。因此FPS带来的时间开销被进一步降低。

temporal conv

由于时间维的结构很规则，因此直接用类似一维卷积的方法即可。

被选中的、会被移动到时域卷积核中心的帧都是时域锚定帧（temporal anchor frames）。通过锚点的传递，可以得到一个四维圆柱（point cube）的结构，可以看成PST总体的“核”所能占据的范围（尽管时间核和空间核是分步计算的）。

总体的卷积过程可以参考下图（图源原文）：

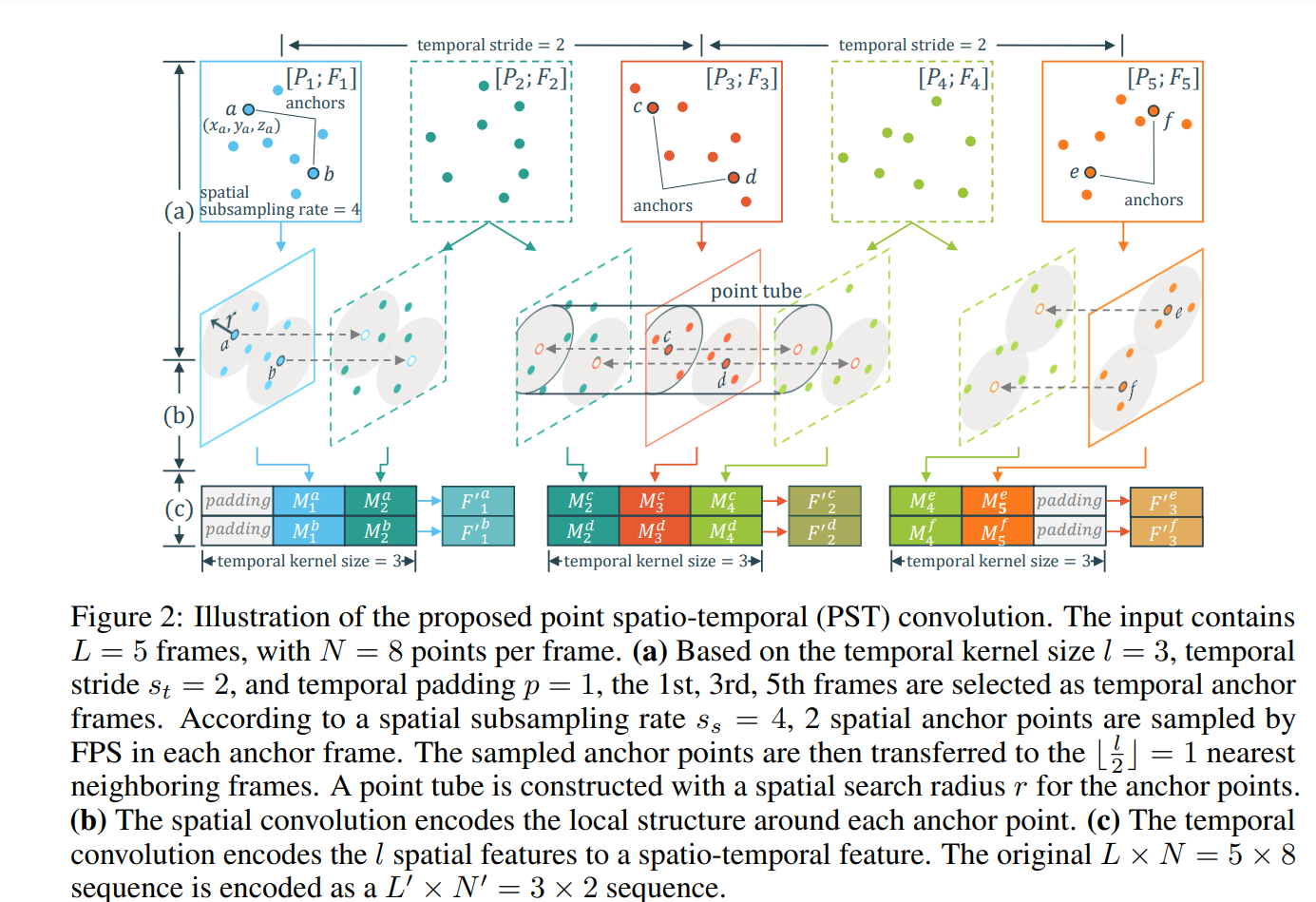
Transposed PST

在语义分割之类的任务中，需要对每个点生成特征向量，这就需要转置卷积（transposed conv，deconv）使点恢复。原论文中也给出了PST转置的方法，这里省略。