对顶点采样

简单介绍几种获取点云的采样方法

Random Sampling

从点云或mesh的顶点集直接随机抽样，获得点云。

这种最自然的想法的问题是：由于随机性，点的分布可能在某些局部是“一簇一簇”的。换言之，点的分布其实不够均匀。

Uniform Sampling

从mesh的各个面片上均匀抽取点。其方法为（假设为三角mesh）：

估计总面积和各面片的面积，根据比例关系确定各个面片上究竟各需要采多少个点。
在一个三角形区域内均匀采样。

Uniform Sampling in a Triangle

在三角形 $\Delta ABC$ 内均匀采样的一种错误方法：

从[0,1]均匀分布中抽取三个值 $a,b,c$
归一化： $a'=a/(a+b+c),b'=b/(a+b+c),c'=c/(a+b+c)$
$P=a'A+b'B+c'C$

可以证明：这样得到的 $P$ 其实不是均匀分布，而是在三角形中心更加集中。

正确的方法是：

先把 $\Delta ABC$ 转化为平行四边形 $ABDC$ ，其中 $D$ 是 $A$ 关于 $BC$ 所在直线的对称点。
从[0,1]均匀分布抽取2个值，并归一化得到 $a',b'$
$P=A+a'(B-A)+b'(C-A)$ ，当 $P$ 不在 $\Delta ABC$ 中时，就使用其关于 $BC$ 所在直线的对称点。

容易证明，此时抽出的点 $P$ 在平行四边形内是均匀分布的，因此对称后在三角形中还是均匀分布。

如下图所示，左图为错误方法，右图为正确方法（图源：Geography meets ML）。

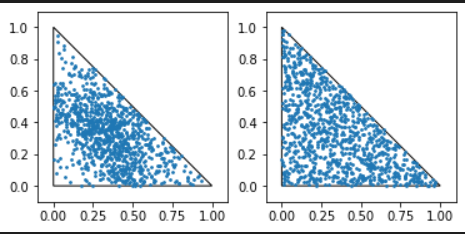
需要注意的是，均匀采样仍然带有随机性，因此采出来的点还是不太均匀。

Farthest Point Sampling

这是一种基于“最大化点之间距离”从而使点分布均匀的采样方法。当然，实际使用时采用的是迭代近似的方案。

首先需要定义点到点集（点云）的距离为点到点集中所有点距离中的最小值。

先用Uniform Sampling等方法，得到一个初始点云 $U$ ，但 $U$ 的点数远多于目标点数（如10倍）
令 $S=\{\}$ 。
令 $T$ 代表 $U$ 中各点到当前 $S$ （点集）的距离表。初始化 $T$ 为 $+\infin$ （由于一开始 $S$ 是空的）。
随机选择一个点 $P$ 。
把 $P$ 放入 $S$ 中。如果 $S$ 的大小已经达到目标点数，则退出。
计算 $P$ 点到 $U$ 中所有点的距离，并将其与 $T$ 的对应各个距离值取较小值来更新 $T$ 。
选择到 $S$ 距离最大的点 $P$ ，即 $T$ 中最大值所对应的点（由于已经在 $S$ 的点到 $S$ 的距离就是0，因此不会被重复选择）
返回第5步。

可以参考的简单代码实现：

import numpy as np
def FPS(ptcloud,count):
    #省略了获取初始点云的过程
    U = ptcloud
    S = []
    dist_to_S = np.full(len(U),np.inf)	#即距离表T
    newpt_idx = 0	#这里没随机选择，而是直接取了第一个点，效果应当差不多
    for _ in range(count):
        S.append(U[newpt_idx])
        dist_offer = np.sum((U - U[newpt_idx])**2,axis=1)
        dist_to_S = np.min(np.stack((dist_offer,dist_to_S)),axis=0)
        #找新点
        newpt_idx = np.argmax(dist_to_S)
    return np.array(S)
#使用例
ptcloud_fps = FPS(ptcloud,4000)

复杂度

设 $U$ 共有 $N$ 个点，目标点数为 $K$ ，则每次循环会执行 $O(N)$ 次计算（更新距离表），因此总复杂度为 $O(NK)$ 。

Voxel Sampling

即将空间栅格化，每个空间小格随机取一个点。可以分桶实现，于是复杂度为线性。

按：这种方法和图像采样问题有相似之处。