估计曲率的Rusinkiewicz法

对各顶点已经有法向量信息的点云或mesh，可以使用该方法估计一个区域附近的Shape Operator，进而得到主曲率等二阶信息。

下面以三角mesh中求Shape Operator为例，简要介绍这种方法。

Assumption

在每个小三角形中：

1. 有一个局部的参数化映射$f$和对应的参数域定义域$U$，使得$f(U)$就是这个小三角区。
2. 三角形三个顶点切平面近似平行（每个顶点上的法向量（预先给定）未必平行，因此是“近似平行”）。
3. 存在局部映射$f$使得三个顶点的切平面（同时也近似是这三个点构成的平面）中的基底$f_u,f_v$是单位正交基，即第一基本形是二阶单位阵。

Derivation

由假设有$S=(df^Tdf)^{-1}df^TdNdf=df^TdNdf$。

则对某个使用单位正交基$f_u,f_v$的切平面内某条向量的二维坐标表示$X\in\mathbb{R}^2$，有

$Sdf^TdfX=df^TdNdfdf^TdfX=df^TdNdfX$

记$Y=dfX\in \mathbb{R}^3,\Delta n = dNY$，即有：

$Sdf^TY=df^T\Delta n$（*）

这刻画了向某方向移动一个微元位移$Y$后，法向量的变化量（即$\Delta n$）。

Estimation

我们把三个顶点记为$p_0,p_1,p_2$，点上的单位法向量记为$n_0,n_1,n_2$，这个公共切平面的单位正交基为$\xi_u,\xi_v$，则可以得到相应的微元位移$e_0=p_2-p_1$（对应上面的$Y$）和单位法向量变化量，于是列出过定的方程组，再最小二乘法等得到一个对$S$的估计，再用这个估计求主曲率等各种参数。（参考下图。图源：ML Meets Geometry）

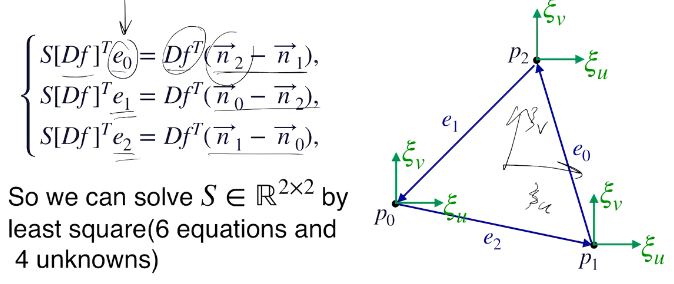
Less Assumption

其实假设三（第一基本形是单位阵）这个要求是完全没有必要理会的。没有这条假设的情况下，精确的（*）式为$S^Tdf^TY=df^T\Delta n$。因此用上面的估计方法可以得到对Shape Operator转置的估计，如果要得到$S$只用转置回来就成；如果只是估计主曲率等等，则由于转置矩阵和原矩阵有相同的特征值，于是连这步多余的“转置”操作也不需要。、

推导：

$LHS$

$=S^Tdf^TY=df^TdNdf(df^Tdf)^{-1}df^TdfX=df^TdNdfX=df^T\Delta n$

$=RHS$